题目内容
3.关于x,y的方程$\frac{x^2}{5-m}+\frac{y^2}{2+m}=1$满足下列曲线,分别求m的取值范围:(1)焦点在x轴的椭圆;
(2)焦点在y的双曲线.
分析 (1)由题意可得$\left\{{\begin{array}{l}{5-m>0}\\{2+m>0}\\{5-m>2+m}\end{array}}\right.$,求解不等式组得答案;
(2)由题意可得$\left\{{\begin{array}{l}{5-m<0}\\{2+m>0}\end{array}}\right.$,求解不等式组得答案.
解答 解:(1)∵方程$\frac{x^2}{5-m}+\frac{y^2}{2+m}=1$表示焦点在x轴的椭圆,
∴$\left\{{\begin{array}{l}{5-m>0}\\{2+m>0}\\{5-m>2+m}\end{array}}\right.$,解得:$-2<m<\frac{3}{2}$;
(2)∵方程$\frac{x^2}{5-m}+\frac{y^2}{2+m}=1$表示焦点在y的双曲线,
∴$\left\{{\begin{array}{l}{5-m<0}\\{2+m>0}\end{array}}\right.$,解得:m>5.
点评 本题考查曲线与方程,考查了椭圆与双曲线的标准方程,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.某几何体的三视图如图所示,则该几何体的体积是( )


| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
8.由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x-y+2≥0}\end{array}\right.$确定的平面区域记为Ω1,不等式组$\left\{\begin{array}{l}{x+y-1≤0}\\{x+y+2≥0}\end{array}\right.$确定的平面区域记为Ω2,在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
15.如图,正方体ABCD-A1B1C1D1中,点E,F分别是AA1,AD的中点,则CD1与EF所成角为( )
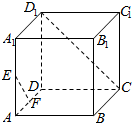

| A. | 0° | B. | 45° | C. | 60° | D. | 90° |
12.在空间四边形ABCD中,$\overrightarrow{DA}=\overrightarrow a,\overrightarrow{DB}=\overrightarrow b,\overrightarrow{DC}=\overrightarrow c$,P在线段AD上,且DP=2PA,Q为BC的中点,则$\overrightarrow{PQ}$=( )
| A. | $\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b-\frac{1}{2}\overrightarrow c$ | B. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b-\frac{2}{3}\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a-\frac{2}{3}\overrightarrow b+\frac{1}{2}\overrightarrow c$ | D. | $-\frac{2}{3}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$ |