题目内容
2.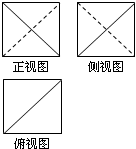 已知一个空间几何体的三视图如图所示,其三视图均为边长为1的正方形,则这个几何体的表面积为3+$\sqrt{3}$.
已知一个空间几何体的三视图如图所示,其三视图均为边长为1的正方形,则这个几何体的表面积为3+$\sqrt{3}$.
分析 该几何体为边长为1正方体截去两个三棱锥得到的,作出直观图代入数据计算即可.
解答 解:由三视图可知几何体为边长为1正方体ABCD-A'B'C'D'截去三棱锥D-ACD'和三棱锥B-ACB'得到的,作出直观图如图所示: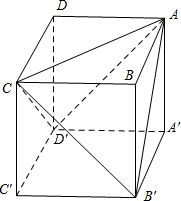
该几何体由前,后,左,右,下和两个斜面组成.
其中前后左右四个面均为直角边为1的等腰直角三角形,底面为边长为1的正方形,两个斜面为边长为$\sqrt{2}$的等边三角形,
∴S=$\frac{1}{2}×4$+1+$\frac{\sqrt{3}}{4}$×($\sqrt{2}$)2×2=3+$\sqrt{3}$.
故答案为$3+\sqrt{3}$.
点评 本题考查了不规则几何体的三视图及面积计算,将不规则几何体转化到正方体中是解题关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
17.多面体的直观图如图所示,则其正视图为( )


| A. |  | B. |  | C. |  | D. |  |
14.某几何体的三视图如图所示,则该几何体的体积是( )


| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
12.在空间四边形ABCD中,$\overrightarrow{DA}=\overrightarrow a,\overrightarrow{DB}=\overrightarrow b,\overrightarrow{DC}=\overrightarrow c$,P在线段AD上,且DP=2PA,Q为BC的中点,则$\overrightarrow{PQ}$=( )
| A. | $\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b-\frac{1}{2}\overrightarrow c$ | B. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b-\frac{2}{3}\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a-\frac{2}{3}\overrightarrow b+\frac{1}{2}\overrightarrow c$ | D. | $-\frac{2}{3}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$ |
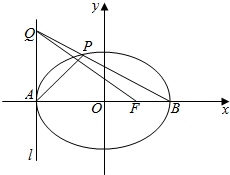 如图,A、B分别是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(2>b>0)的左右顶点,F为其右焦点,|AF|×|FB|=3.
如图,A、B分别是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(2>b>0)的左右顶点,F为其右焦点,|AF|×|FB|=3.