题目内容

证明：函数f（x）=2x3-6x2在（0，2）内是减函数．
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：先求出f′（x）=6x2-12x，令f（x）＜0，解得：0＜x＜2，从而证得函数f（x）=2x3-6x2在（0，2）内是减函数．
解答： 证明：∵f′（x）=6x2-12x，
令f（x）＜0，解得：0＜x＜2，
∴函数f（x）=2x3-6x2在（0，2）内是减函数．
点评：本题考察了函数的单调性，导数的应用，是一道基础题．
练习册系列答案
相关题目
如图1，在直角梯形ABCD中，AD∥BC，AD=AB=
2
，∠BAD=90°，∠BCD=45°，E为对角线BD的中点．现将△ABD沿BD折起到△PBD的位置，使平面PBD⊥平面BCD，如图2．
（Ⅰ）求证直线PE⊥平面BCD；
（Ⅱ）求异面直线BD和PC所成角的余弦值；
（Ⅲ）已知空间存在一点Q到点P，B，C，D的距离相等，写出这个距离的值（不用说明理由）．
各项均不为零的数列{an}的前n项和为Sn，且an+3SnSn-1=0（n≥2），a1=
1
3
．
（1）求数列{an}的通项公式an；
（2）若bn=
1 ，(n=1)
1
3(1-n)an
，(n≥2)
，设Tn=
1
b1+n
+
1
b2+n
+…+
1
bn+n
，若Tn＞m对n≥2恒成立，求实数m的取值范围．
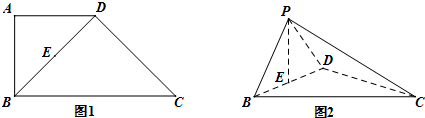
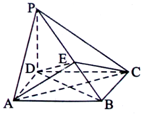如图，在四棱椎P-ABCD中，PD⊥平面ABCD，四边形ABCD是边长为2的菱形，∠ABC=
2π
3
，PD=2
3
，E是PB的中点．
（Ⅰ）求证：平面AEC⊥平面PDB；
（Ⅱ）求三棱锥D-BCE的体积VD-BCE．
已知等差数列{an}的公差大于0，且a3，a5是方程x2-14x+45=0的两根，数列{bn}的前n项的和为Sn，且Sn=1-
1
2
bn．
（1）求数列{an}，{bn}的通项公式；  
（2）记cn=an•bn，求数列{cn}的前n项和Tn．
已知x=1是函数f(x)=2x+
a
x
+lnx的一个极值点，
（1）求a的值；
（2）求函数f（x）的单调区间．
已知函数f（x）的导函数为f′（x），且f（x）=2xf′（1）+lnx，则f′（x）=
 
．
已知函数f（x），其中x∈R，f（1）=2，且f（x）在R上的导数满足f′（x）＜1，则不等式f（x2）＜x2+1的解集为
 
．
已知函数y=Asin（ωx+φ）（A＞0，ω＞0，0≤φ＜π）的部分图象如图所示，则A=
 
，ω=
 
，φ=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网