题目内容
如果复数z=2-ai满足条件|z-1|<2,那么实数a的取值范围为( )
A、(-2
| ||||
| B、(-2,2) | ||||
| C、(-1,1) | ||||
D、(-
|
考点:复数求模
专题:转化思想,数系的扩充和复数
分析:利用模的定义,从两个已知条件中消去z,再由得数的模的公式转化为转化a的不等式,解出a的取值范围;
解答:
解:∵z=2-ai(a∈R),|z-1|<2,得|2-ai-1|<2,即|1-ai|<2,
即
<2
解得-
<a<
.
故选:D.
即
| 1+a2 |
解得-
| 3 |
| 3 |
故选:D.
点评:本题考查复数的代数表示法及其几何意义,解题的关键是理解复数的代数形式及其几何意义,将问题转化不等式求解或将问题转化为图象利用几何关系求解,本题考查了转化的思想,数形结合的思想,是复数中较为典型的题,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
圆(x-1)2+(y+3)2=2的圆心和半径分别为( )
| A、(-1,3),2 | ||
B、(1,-3),
| ||
| C、(1,-3),2 | ||
D、(-1,3),
|
已知{an}是等差数列,Sn为其前n项和,若S21=S4000,O为坐标原点,点P(2,an)、Q(2011,a2011),则
•
=( )
| OP |
| OQ |
| A、4022 | B、2011 |
| C、0 | D、1 |
已知cosα=
,cosβ=
,且α,β∈(0,
),则cos(α-β)=( )
| 1 |
| 3 |
| 7 |
| 9 |
| π |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|




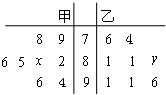 某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则x+y的值为( )
某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则x+y的值为( )