题目内容
2.已知等差数列{an}满足a3=7,a3+a7=26.(1)求数列{an}的通项公式;
(2)令${b_n}=\frac{2n}{{{a_n}-8}}$(n∈N*),求数列{bn}的最大项和最小项.
分析 (1)利用等差数列的通项公式即可得出.
(2)由(1)知:${b_n}=\frac{2n}{2n-7}=1+\frac{7}{2n-7}$,利用单调性即可得出.
解答 解:(1)由题意$\left\{\begin{array}{l}{{a_3}={a_1}+2d=7}\\{{a_5}+{a_7}=2{a_1}+10d=26}\end{array}⇒\left\{\begin{array}{l}{d=2}\\{{a_1}=3}\end{array}$,
所以an=2n+1
(2)由(1)知:${b_n}=\frac{2n}{2n-7}=1+\frac{7}{2n-7}$
又因为当n=1,2,3时,数列{bn}递减且$\frac{7}{2n-7}<0$;
当n≥4时,数列{bn}递减且$\frac{7}{2n-7}>0$;
所以,数列{bn}的最大项为b4=8,最小项为b3=-6
点评 本题考查了等差数列的通项公式、单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
12. 如图,在平行四边形ABCD中,AB=1,AD=2,点E,F,G,H分别是AB,BC,CD,DA边上的中点,则$\overrightarrow{EF}•\overrightarrow{FG}+\overrightarrow{GH}•\overrightarrow{HE}$=( )
如图,在平行四边形ABCD中,AB=1,AD=2,点E,F,G,H分别是AB,BC,CD,DA边上的中点,则$\overrightarrow{EF}•\overrightarrow{FG}+\overrightarrow{GH}•\overrightarrow{HE}$=( )
 如图,在平行四边形ABCD中,AB=1,AD=2,点E,F,G,H分别是AB,BC,CD,DA边上的中点,则$\overrightarrow{EF}•\overrightarrow{FG}+\overrightarrow{GH}•\overrightarrow{HE}$=( )
如图,在平行四边形ABCD中,AB=1,AD=2,点E,F,G,H分别是AB,BC,CD,DA边上的中点,则$\overrightarrow{EF}•\overrightarrow{FG}+\overrightarrow{GH}•\overrightarrow{HE}$=( )| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $-\frac{3}{4}$ |
10.已知$\frac{1-tanα}{1+tanα}$=2+$\sqrt{3}$,则tan($\frac{π}{4}$+α)等于( )
| A. | 2+$\sqrt{3}$ | B. | 1 | C. | 2-$\sqrt{3}$ | D. | $\sqrt{3}$ |
7.△ABC的三内角A,B,C所对边的长分别是a,b,c,若$\frac{sinB-sinA}{sinC}=\frac{{\sqrt{2}a+c}}{a+b}$,则角B的大小为( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
12.已知函数f(x)=x3-3x2-m存在2个零点,则这两个零点的和为( )
| A. | 1 | B. | 3 | C. | 1或4 | D. | 1或3 |
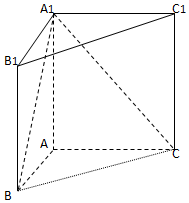 如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.
如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.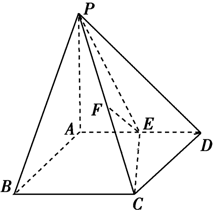 如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E、F分别为棱AD、PC的中点.
如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E、F分别为棱AD、PC的中点.