题目内容
10.已知$\frac{1-tanα}{1+tanα}$=2+$\sqrt{3}$,则tan($\frac{π}{4}$+α)等于( )| A. | 2+$\sqrt{3}$ | B. | 1 | C. | 2-$\sqrt{3}$ | D. | $\sqrt{3}$ |
分析 由条件利用两角和差的正切公式,求得要求式子的值.
解答 解:∵已知$\frac{1-tanα}{1+tanα}$=2+$\sqrt{3}$,则tan($\frac{π}{4}$+α)=$\frac{1+tanα}{1-tanα}$=$\frac{1}{\frac{1-tanα}{1+tanα}}$=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$,
故选:C.
点评 本题主要考查两角和差的正切公式的应用,属于基础题.

练习册系列答案
相关题目
1.若如图所示的程序框图输出的y=2,可输入的x的值的个数为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
18.若sinx+cosx=$\frac{1}{5}$,0<x<π,则tanx的值是( )
| A. | $\frac{4}{3}或-\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}或-\frac{3}{4}$ |
5.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的右焦点为F,上顶点为A,若直线AF与圆O:${x^2}+{y^2}=\frac{{3{a^2}}}{16}$相切,则该椭圆的离心率为( )
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$或$\frac{{\sqrt{3}}}{2}$ |
15.若 (2x-1)2017=a0+a1x+a2x2+…+a2017x2017(x∈R),则$\frac{1}{2}+\frac{a_2}{{{2^2}{a_1}}}+\frac{a_3}{{{2^3}{a_1}}}+…+\frac{{{a_{2017}}}}{{{2^{2017}}{a_1}}}$=( )
| A. | $\frac{1}{2017}$ | B. | $-\frac{1}{2017}$ | C. | $\frac{1}{4034}$ | D. | $-\frac{1}{4034}$ |
19.已知直线l1:(3+m)x+4y=4,l2:2x+(5+m)y=8平行,实数m的值为( )
| A. | -7 | B. | -1 | C. | $\frac{13}{3}$ | D. | -1或-7 |
20.已知复数z1=3+4i,z2=3-4i,则z1+z2=( )
| A. | 8i | B. | 6 | C. | 6+8i | D. | 6-8i |
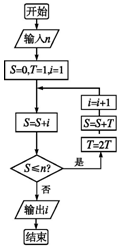 执行如图所示的程序框图,当输出i的值是4时,输入的整数n的最大值是23.
执行如图所示的程序框图,当输出i的值是4时,输入的整数n的最大值是23.