题目内容
设f(x)=22x-5×2x-1+1,它的最小值是 .
考点:函数的最值及其几何意义
专题:
分析:通过观察,可将原函数变成一个式子的平方,即变成(2x-
)2-
,到这显然看出2x-
=0时,原函数取得最小值,最小值是-
.
| 5 |
| 4 |
| 9 |
| 16 |
| 5 |
| 4 |
| 9 |
| 16 |
解答:
解:f(x)=22x-5×2x-1+1=(2x-
)2-
,
所以(2 x-
)2=0,即2x-5=0,x=log2
时,原函数取到最小值-
.
故答案为:-
.
| 5 |
| 4 |
| 9 |
| 16 |
所以(2 x-
| 5 |
| 4 |
| 5 |
| 4 |
| 9 |
| 16 |
故答案为:-
| 9 |
| 16 |
点评:本题主要是能看出存在的一个完全平方式,只要配成平方的形式,本题的答案就显而易见了.

练习册系列答案
相关题目
若C
=C
,则n=( )
2n-5 11 |
n+1 11 |
| A、5 | B、6 | C、5或2 | D、5或6 |
 已知某几何体的三视图如图所示,其中正视图与侧视图都是直角边为2的等腰直角三角形,则该几何体的表面积为
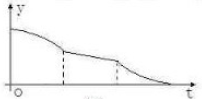
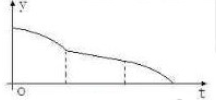
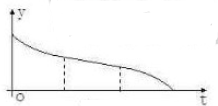
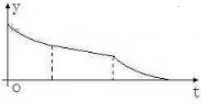
已知某几何体的三视图如图所示,其中正视图与侧视图都是直角边为2的等腰直角三角形,则该几何体的表面积为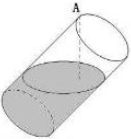 一空的圆柱体容器直径小于母线长斜放,将容器斜放,使圆柱的母线与水平面成45°角,现于这种状态下由容器的最高点A处匀速地灌油,如图,则点A到油平面的距离y与灌水时间t的函数图象大致为( )
一空的圆柱体容器直径小于母线长斜放,将容器斜放,使圆柱的母线与水平面成45°角,现于这种状态下由容器的最高点A处匀速地灌油,如图,则点A到油平面的距离y与灌水时间t的函数图象大致为( )