题目内容
正三角形ABC的边长为a,利用斜二测画法得到的平面直观图为△A′B′C′,那么△A′B′C′的面积为 .
考点:平面图形的直观图
专题:空间位置关系与距离
分析:斜二测画法得到的平面直观图的面积等于原图形面积乘以
.
| ||
| 4 |
解答:
解:∵正三角形ABC的边长为a,
∴S△ABC=
a•a•sin60°=
a2,
∴S△A′B′C′=
×
a2=
a2.
故答案为:
a2.
∴S△ABC=
| 1 |
| 2 |
| ||
| 4 |
∴S△A′B′C′=
| ||
| 4 |
| ||
| 4 |
| ||
| 16 |
故答案为:
| ||
| 16 |
点评:本题考查斜二测画法得到的平面直观图的面积的求法,是基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
正方体ABCD-A1B1C1D1中,M、N分别是棱DD1和BB1上的点,MD=
DD1,NB=
BB1,那么正方体的过M、N、C1的截面图形是( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、三角形 | B、四边形 |
| C、五边形 | D、六边形 |
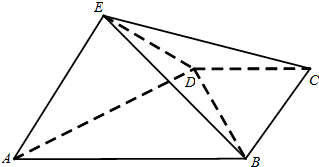 如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.
如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2. 如图,四面体D-ABC的体积为
如图,四面体D-ABC的体积为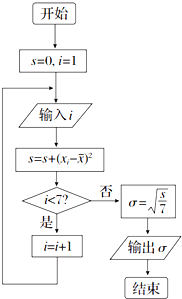 在2012~2013赛季NBA季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如表:
在2012~2013赛季NBA季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如表: