题目内容
函数f(x)=log2
•log
(2x)•log
(2x)的最小值为 .
| 2 |
| 2 |
| 2 |
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:根据对数的基本运算法则即可得到结论.
解答:
解:f(x)=log2
•log
(2x)•log
(2x)=
(log
2+log
x)2=
(2+log
x)2,
∴当log
x=-2,即x=
时,函数f(x)取得最小值为0.
故答案为:0
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
∴当log
| 2 |
| 1 |
| 2 |
故答案为:0
点评:本题主要考查函数的最值的求解,根据对数函数的基本运算法则进行化简是解决本题的关键.

练习册系列答案
相关题目
已知点P(x,y)在圆(x+2)2+y2=3上,则
的最小值为( )
| y |
| x |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
下列命题正确的是( )
| A、ac<bc⇒a<b | ||||
| B、a<b⇒lga<lgb | ||||
C、
| ||||
D、
|
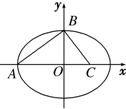 如图,A、B、C分别为椭圆
如图,A、B、C分别为椭圆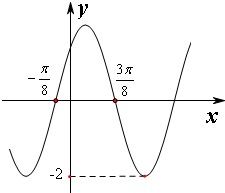 已知函数f(x)=Asin(ωx+ϕ),(A>0,ω>0,0≤ϕ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=
已知函数f(x)=Asin(ωx+ϕ),(A>0,ω>0,0≤ϕ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=