题目内容
△ABC是等腰直角三角形,已知A(1,1),B(1,3),AB⊥BC,点C在第一象限,点(x,y)在△ABC内部,则点C的坐标为 ,z=2x-y的最大值是 .
考点:简单线性规划
专题:不等式的解法及应用
分析:根据等腰直角三角形的定义先求出C的坐标,利用线性规划的知识即可得到结论.
解答:
解:∵A(1,1),B(1,3),AB⊥BC,点C在第一象限,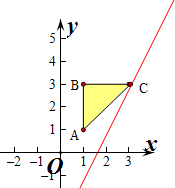
∴|AB|=3-1=2,
设C(x,y),则x>0,y>0,
∵△ABC是等腰直角三角形,
∴|BC|=|x-1|=2,解得x=3或x=-1(舍),
即C(3,3),
由z=2x-y得y=2x-z,
平移直线y=2x-z,由图象可知当直线y=2x-z经过点C时,直线y=2x-z的截距最小,此时z最大,
此时z=2x-y=2×3-3=3,
故答案为:(3,3),3

∴|AB|=3-1=2,
设C(x,y),则x>0,y>0,
∵△ABC是等腰直角三角形,
∴|BC|=|x-1|=2,解得x=3或x=-1(舍),
即C(3,3),
由z=2x-y得y=2x-z,
平移直线y=2x-z,由图象可知当直线y=2x-z经过点C时,直线y=2x-z的截距最小,此时z最大,
此时z=2x-y=2×3-3=3,
故答案为:(3,3),3
点评:本题主要考查线性规划的应用,利用数形结合是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若a=9,b=12,A=45°,则△ABC有( )
| A、一解 | B、两解 |
| C、无解 | D、不能确定 |
已知命题p:?a∈R,且a>0,a+
≥2,命题q:不等式(2-x)(x+1)<0的解集是(-1,2),则下列判断正确的是( )
| 1 |
| a |
| A、p是假命题 |
| B、q是真命题 |
| C、p∧(¬q)是真命题 |
| D、(¬p)∨q是真命题 |
等差数列{an}中,若a3+a7=8,则a2+a3+a4+a5+a6+a7+a8=( )
| A、24 | B、32 | C、28 | D、35 |
 如图在△ABC中,AB=2,AC=3,D为BC的中点,则向量
如图在△ABC中,AB=2,AC=3,D为BC的中点,则向量