题目内容
椭圆2x2+3y2=6的焦距是( )
| A、2 | ||||
B、2(
| ||||
C、2
| ||||
D、2(
|
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:把椭圆的方程化为标准形式,求出a、b、c的值,可得焦距2c的值.
解答:
解:椭圆2x2+3y2=6可化为
+
=1,
∴c=
=1,
∴椭圆2x2+3y2=6的焦距是2c=2,
故选:A.
| x2 |
| 3 |
| y2 |
| 2 |
∴c=
| 3-2 |
∴椭圆2x2+3y2=6的焦距是2c=2,
故选:A.
点评:本题考查椭圆的标准方程以及椭圆的简单性质的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设全集为R,集合A={x|x2-9<0},B={x|-1<x≤5},则A∩B=( )
| A、(3,5] |
| B、(-1,3) |
| C、(-3,-1) |
| D、(-3,5] |
已知集合M={x|log3x≤1},N={x|x2-2x<0},则( )
| A、M=N | B、M∩N=∅ |
| C、M∩N=R | D、N⊆M |
已知{an}是等差数列,a1+a7=-2,a3=2,则{an}的公差d=( )
| A、-1 | B、-2 | C、-3 | D、-4 |
函数y=lg(-x2-3x+4)的定义域是( )
| A、(-4,-1) |
| B、(-4,1) |
| C、(-1,4) |
| D、[-4,1] |
等差数列{an}中,a1+a4+a7=39,a2+a5+a8=33,则a6的值为( )
| A、10 | B、9 | C、8 | D、7 |
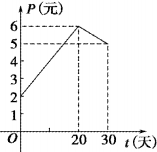 某上市股票在30填内每股交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上,该股票在30填内的日交易量Q(万股)与时间t(天)的部分数据如表所示:
某上市股票在30填内每股交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上,该股票在30填内的日交易量Q(万股)与时间t(天)的部分数据如表所示: