题目内容
 如图,设A(2,4)是抛物线C:y=x2上的一点.
如图,设A(2,4)是抛物线C:y=x2上的一点.(1)求该抛物线在点A处的切线l的方程;
(2)求曲线C、直线l和x轴所围成的图形的面积.
考点:定积分在求面积中的应用,利用导数研究曲线上某点切线方程
专题:综合题,导数的概念及应用
分析:(1)求导数,可得切线斜率,从而可得该抛物线在点A处的切线l的方程;
(2)利用定积分可求曲线C、直线l和x轴所围成的图形的面积.
(2)利用定积分可求曲线C、直线l和x轴所围成的图形的面积.
解答:
解:(1)∵y=x2,∴y′=2x-------------------------------2分
∴直线?的斜率k=y/|_x=2 =4---------------------------------------4分
∴l:y-4=4(x-2),即y=4x-4为所求.----------------7分,
(2):法一:切线y=4x-4与x轴的交点为B(1,0),
则面积S=
x2dx+
[x2-(4x-4)]dx=
-------------------------------13分
法二:面积S=
(
+1-
)dy=(
y2+y-
×y
)
=
,
∴曲线C、直线l和x轴所围成的图形的面积为
.
∴直线?的斜率k=y/|_x=2 =4---------------------------------------4分
∴l:y-4=4(x-2),即y=4x-4为所求.----------------7分,
(2):法一:切线y=4x-4与x轴的交点为B(1,0),
则面积S=
| ∫ | 1 0 |
| ∫ | 2 1 |
| 2 |
| 3 |
法二:面积S=
| ∫ | 4 0 |
| y |
| 4 |
| y |
| 1 |
| 8 |
| 2 |
| 3 |
| 2 |
| 3 |
|
| 2 |
| 3 |
∴曲线C、直线l和x轴所围成的图形的面积为
| 2 |
| 3 |
点评:本题考查导数的几何意义,考查了定积分在求面积中的应用,以及定积分的计算,属于基础题.

练习册系列答案
相关题目
 (理)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AB=AC=1,∠ABC=
(理)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AB=AC=1,∠ABC= 三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.
三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.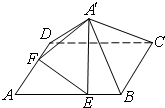 如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2