题目内容
18.已知过抛物线y2=4x的焦点F的直线l交抛物线于A,B两点.(Ⅰ)求F点坐标;
(Ⅱ)试问在x轴上是否存在一点T(不与F重合),使∠ATF=∠BTF?若存在,求出T点坐标;若不存在,请说明理由.
(Ⅲ)若P是抛物线上异于A,B的任意一点,l1是抛物线的准线,直线PA、PB分别交l1于点M、N,求证:$\overrightarrow{OM}$•$\overrightarrow{ON}$为定值,并求出该定值.
分析 (Ⅰ)由抛物线方程知F(1,0);
(Ⅱ)设直线l的方程为x=my+1,将抛物线C的方程y2=4x与直线l的方程联立,设A(x1,y1),B(x2,y2),由韦达定理求得kAT+kBT,设点T(a,0)存在,由TA,TB与x轴所成的锐角相等可得kTA+kTB=0,利用韦达定理,即可求得a;
(Ⅲ)求出M,N点横坐标,利用向量的数量积公式,即可得出结论.
解答 解:(Ⅰ)抛物线方程知F(1,0);
(Ⅱ)设A(x1,y1),B(x2,y2),设直线l的方程为x=my+1(m≠0),
代入y2=4x得y2-4my-4=0,△=16m2+16>0恒成立,
$\left\{\begin{array}{l}{{y}_{1}+{y}_{2}=4m}\\{{y}_{1}{y}_{2}=-4}\end{array}\right.$
假设存在T(a,0)满足题意,则kAT+kBT=$\frac{{y}_{1}}{{x}_{1}-a}+\frac{{y}_{2}}{{x}_{2}-a}=\frac{2m{y}_{1}{y}_{2}+(1-a)({y}_{1}+{y}_{2})}{{(x}_{1}-a)({x}_{2}-a)}$=0
∴-8m+4m(1-a)=0,
∴a=-1,∴存在T(-1,0);
(Ⅲ)设P(x0,y0),则直线PA的方程为:y-y1=$\frac{4}{{y}_{1}+{y}_{0}}(x-{x}_{1})$
当x=-1时,y=$\frac{{y}_{1}{y}_{0}-4}{{y}_{1}+{y}_{0}}$,即M点纵坐标为yM=$\frac{{y}_{1}{y}_{0}-4}{{y}_{1}+{y}_{0}}$,
同理可得N点纵坐标为yN=$\frac{{y}_{2}{y}_{0}-4}{{y}_{2}+{y}_{0}}$.
∴yMyN=$\frac{{y}_{1}{y}_{0}-4}{{y}_{1}+{y}_{0}}$×$\frac{{y}_{2}{y}_{0}-4}{{y}_{2}+{y}_{0}}$=$\frac{{y}_{1}{y}_{0}+{y}_{1}{y}_{2}}{{y}_{1}+{y}_{0}}•\frac{{y}_{2}{y}_{0}+{y}_{1}{y}_{2}}{{y}_{2}+{y}_{0}}={y}_{1}{y}_{2}=-4$
∴$\overrightarrow{OM}•\overrightarrow{ON}$═yMyN+(-1)•(-1)=-3为定值
点评 本题考查抛物线的简单性质,考查直线与抛物线的位置关系,考查向量的数量积公式,属于中档题.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案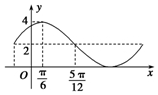
| A. | A=4 | B. | ω=1 | C. | φ=$\frac{π}{6}$ | D. | B=4 |
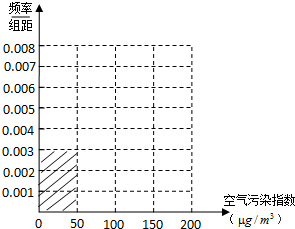
| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
(Ⅱ)在空气污染指数分别为50~100和150~200的监测点中,用分层抽样的方法抽取10个监测点,从中任意选取4个监测点,求这4个监测点中空气质量为良的个数ξ的期望.
| A. | y2=-x | B. | y2=2x | C. | 2x2=y | D. | x2=-4y |
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |