题目内容
给出四个函数;(1)y=x3+x(2)y=
(x>0)(3)y=
(4)y=x2+1,其中奇函数的个数是( )
| 1 |
| x |
| x2+2 |
| x |
| A、1 | B、2 | C、3 | D、4 |
考点:函数奇偶性的判断
专题:计算题,函数的性质及应用
分析:利用奇偶函数的定义,即可得出结论.
解答:
解:(1)y=x3+x是奇函数;
(2)y=
(x>0),定义域不关于原点对称,不是奇函数;
(3)y=
是奇函数;
(4)y=x2+1是偶函数,
故选:B.
(2)y=
| 1 |
| x |
(3)y=
| x2+2 |
| x |
(4)y=x2+1是偶函数,
故选:B.
点评:本题考查函数奇偶性的判断,考查学生对概念的理解,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知y=f(x)是定义在R上的奇函数,当x>0时,f(x)=x-2,那么不等式f(x)<0的解集是( )
| A、(0,+∞) |
| B、(-2,2) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-∞,-2)∪(0,2) |
对于正整数a,若存在正整数b,使得a=bn(n∈N+)则a是n次方数,其中2次方数也叫平方数,则“正整数a是平方数”是“正整数a是4次方数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在{an}为等比数列中,an>0,a2a4+2a3a5+a52=16,那么a3+a5=( )
| A、±4 | B、4 | C、2 | D、8 |
若a=20.3,b=sin1,c=log30.2,则( )
| A、b>c>a |
| B、b>a>c |
| C、c>a>b |
| D、a>b>c |
设集合A={(x,y)|x∈N,y∈N},B={(x,y)|x+y=4},则满足C⊆(A∩B)的集合C的个数是( )
| A、8 | B、16 | C、32 | D、64 |
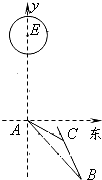 在特定时段内,以点E为中心的5海里以内海域被设为警戒水域.点E正南30海里处有一个雷达观测点A.某时刻测得一艘匀速直线行驶的船只位于点A南偏东45°且与点A相距20
在特定时段内,以点E为中心的5海里以内海域被设为警戒水域.点E正南30海里处有一个雷达观测点A.某时刻测得一艘匀速直线行驶的船只位于点A南偏东45°且与点A相距20