题目内容
已知等差数列{an}(n∈N*)的首项a1>0,设Sn为{an}的前n项和,且S4=S11,则当Sn取得最大值时n的值为 .
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由S4=S11,得S11-S4=a5+a6+a7+a8+a9+a10+a11=7a8=0,从而a8=0,a7>0,由此得到当n=7或n=9时Sn取得最大值.
解答:
解:∵S4=S11,
∴S11-S4=a5+a6+a7+a8+a9+a10+a11=7a8=0,
∴a8=0,
∵a1>0,
∴数列{an}为递减数列,
∴a7>0,
∴当n=7或n=8时Sn取得最大值.
故答案为:7或8.
∴S11-S4=a5+a6+a7+a8+a9+a10+a11=7a8=0,
∴a8=0,
∵a1>0,
∴数列{an}为递减数列,
∴a7>0,
∴当n=7或n=8时Sn取得最大值.
故答案为:7或8.
点评:本题考查数列的前n项和取得最大值时n的值的求法,是中档题,解题时要注意等差数列的性质的合理运用.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
在△ABC中,
2+
•
<0,则△ABC为( )
| AB |
| AB |
| BC |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、锐角或钝角三角形 |
不等式组
表示的平面区域面积是( )
|
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
在△ABC中,下列等式不成立的是( )
A、c=
| ||||
B、
| ||||
| C、asinC=csinA | ||||
D、cosB=
|
| 1+2sin(2π-2)cos(2π-2) |
| A、sin2+cos2 |
| B、cos2-sin2 |
| C、-sin2-cos2 |
| D、sin2-cos2 |
设复数z=-2-i(i为虚数单位),x的共轭复数为
,则
等于( )
. |
| z |
| z+2 | ||
|
| A、1 | B、-1 | C、i | D、-i |
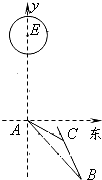 在特定时段内,以点E为中心的5海里以内海域被设为警戒水域.点E正南30海里处有一个雷达观测点A.某时刻测得一艘匀速直线行驶的船只位于点A南偏东45°且与点A相距20
在特定时段内,以点E为中心的5海里以内海域被设为警戒水域.点E正南30海里处有一个雷达观测点A.某时刻测得一艘匀速直线行驶的船只位于点A南偏东45°且与点A相距20