题目内容
已知-4≤a-b≤-1,-1≤4a-b≤5,求9a-b的取值范围.
考点:不等关系与不等式
专题:不等式的解法及应用
分析:设9a-b=m(a-b)+n(4a-b)=(m+4n)a-(m+n)b,解出m,n即可得出.
解答:
解:设9a-b=m(a-b)+n(4a-b)=(m+4n)a-(m+n)b,
∴
,解得m=-
,n=
.
∵-4≤a-b≤-1,-1≤4a-b≤5,
∴
≤-
(a-b)≤
,-
≤
(4a-b)≤
.
∴-1≤9a-b≤20.
∴9a-b的取值范围是[-1,20].
∴
|
| 5 |
| 3 |
| 8 |
| 3 |
∵-4≤a-b≤-1,-1≤4a-b≤5,
∴
| 5 |
| 3 |
| 5 |
| 3 |
| 20 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 40 |
| 3 |
∴-1≤9a-b≤20.
∴9a-b的取值范围是[-1,20].
点评:本题考查了不等式的基本性质,属于基础题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
已知y=f(x)是定义在R上的奇函数,当x>0时,f(x)=x-2,那么不等式f(x)<0的解集是( )
| A、(0,+∞) |
| B、(-2,2) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-∞,-2)∪(0,2) |
在△ABC中,
2+
•
<0,则△ABC为( )
| AB |
| AB |
| BC |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、锐角或钝角三角形 |
如图给出了计算3+5+7+…+19的值的一个程序框图,其中空白处应填入( )


| A、i>9 | B、i>10 |
| C、i>19 | D、i>20 |
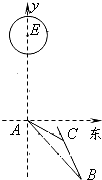 在特定时段内,以点E为中心的5海里以内海域被设为警戒水域.点E正南30海里处有一个雷达观测点A.某时刻测得一艘匀速直线行驶的船只位于点A南偏东45°且与点A相距20
在特定时段内,以点E为中心的5海里以内海域被设为警戒水域.点E正南30海里处有一个雷达观测点A.某时刻测得一艘匀速直线行驶的船只位于点A南偏东45°且与点A相距20