题目内容
圆锥轴截面的顶角是120°,过顶点的截面面积的最大值为8,则它的体积是( )
A、4
| ||
| B、8π | ||
C、8
| ||
| D、24π |
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:作图可知,r=
h,求最大面积时高的值,代入求体积公式求解即可.
| 3 |
解答:
解:则由右图知,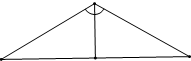 r=
r=
h,
过顶点的截面为等腰三角形,
设底边长为2x,与圆心的距离为d,
则d2+x2=r2,
截面等腰三角形底边上的高为
;
则截面等腰三角形的面积为
S=
•2x•
=x
=x
=
≤
=2h2.
(当且仅当x2=4h2-x2,即x=
h时,等号成立.
则2h2=8,解得,h=2,则r=
h=2
.
则V=
πr2h=
•π•12•2=8π.
故选:B.
 r=
r=| 3 |
过顶点的截面为等腰三角形,
设底边长为2x,与圆心的距离为d,
则d2+x2=r2,
截面等腰三角形底边上的高为
| d2+h2 |
则截面等腰三角形的面积为
S=
| 1 |
| 2 |
| d2+h2 |
=x
| r2-x2+h2 |
=x
| 4h2-x2 |
=
| x2(4h2-x2) |
≤
| x2+4h2-x2 |
| 2 |
(当且仅当x2=4h2-x2,即x=
| 2 |
则2h2=8,解得,h=2,则r=
| 3 |
| 3 |
则V=
| 1 |
| 3 |
| 1 |
| 3 |
故选:B.
点评:本题考查了学生的空间想象力,及基本不等式的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设集合A={(x,y)|x∈N,y∈N},B={(x,y)|x+y=4},则满足C⊆(A∩B)的集合C的个数是( )
| A、8 | B、16 | C、32 | D、64 |
设复数z=-2-i(i为虚数单位),x的共轭复数为
,则
等于( )
. |
| z |
| z+2 | ||
|
| A、1 | B、-1 | C、i | D、-i |
将直线y=
x绕原点顺时针旋转90°,再向左平移1个单位,所得到的直线的方程为( )
| 1 |
| 3 |
| A、y=-3x-3 |
| B、y=-3x+3 |
| C、y=-3x-1 |
| D、y=3x-3 |
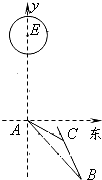 在特定时段内,以点E为中心的5海里以内海域被设为警戒水域.点E正南30海里处有一个雷达观测点A.某时刻测得一艘匀速直线行驶的船只位于点A南偏东45°且与点A相距20
在特定时段内,以点E为中心的5海里以内海域被设为警戒水域.点E正南30海里处有一个雷达观测点A.某时刻测得一艘匀速直线行驶的船只位于点A南偏东45°且与点A相距20