题目内容
19.在△ABC中,内角A,B,C所对的边分别为a,b,c,若a=$\sqrt{3}$,A=60°,B=45°,则b的长为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
分析 由sinA,sinB,以及a的值,利用正弦定理即可求出b的长.
解答 解:∵在△ABC中,内角A,B,C所对的边分别为a,b,c,且a=$\sqrt{3}$,A=60°,B=45°,
∴由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$得:b=$\frac{asinB}{sinA}$=$\frac{\sqrt{3}×\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=$\sqrt{2}$,
故选:C.
点评 此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
10.设等差数列{an}的公差为d,d≠0,若{an}的前10项之和大于其前21项之和,则( )
| A. | d<0 | B. | d>0 | C. | a16<0 | D. | a16>0 |
4.设实数a,b满足|a|>|b|,则“a-b>0”是“a+b>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.函数f(x)=ax3+lnx在区间(0,+∞)上不是单调函数,则a的取值范围是( )
| A. | (-1,1) | B. | (-1,2) | C. | (-∞,0) | D. | (0,+∞) |
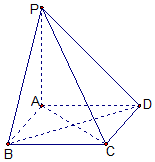 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.求二面角P-CD-B余弦值的大小.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.求二面角P-CD-B余弦值的大小. ,
, ,
,
 B.
B. C.
C. D.
D.