题目内容
14.函数f(x)=ax3+lnx在区间(0,+∞)上不是单调函数,则a的取值范围是( )| A. | (-1,1) | B. | (-1,2) | C. | (-∞,0) | D. | (0,+∞) |
分析 先求导函数,再根据函数在(0,+∞)上不单调,可求a的取值范围.
解答 解:由题意,f′(x)=3ax2+$\frac{1}{x}$=$\frac{3a{x}^{3}+1}{x}$,
∵函数f(x)=ax3+lnx在(0,+∞)上不单调,
∴分子应满足有不等的实根.
∴3a<0,即a<0
故选:C.
点评 本题以函数为载体,考查导数的运用,考查函数的单调性,关键是等价转化.

练习册系列答案
相关题目
19.在△ABC中,内角A,B,C所对的边分别为a,b,c,若a=$\sqrt{3}$,A=60°,B=45°,则b的长为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
9.若方程组$\left\{\begin{array}{l}ax+by=1\\{x^2}+{y^2}=50\end{array}\right.$至少有一解,且所有的解都是整数解,则有序实数对(a,b)的组数为( )
| A. | 60 | B. | 66 | C. | 72 | D. | 78 |
5.已知直线l过抛物线y2=2px(p>0)的焦点F(1,0),交抛物线于M,N两点.
(Ⅰ)写出抛物线的标准方程及准线方程;
(Ⅱ)O为坐标原点,直线MO、NO分别交准线于点P,Q,求|PQ|的最小值.
(Ⅰ)写出抛物线的标准方程及准线方程;
(Ⅱ)O为坐标原点,直线MO、NO分别交准线于点P,Q,求|PQ|的最小值.
2.下列函数中既是奇函数,又在区间(-1,1)上是增函数的为( )
| A. | y=|x+1| | B. | y=sinx | C. | y=2x+2-x | D. | y=lnx |
 ,则满足不等式
,则满足不等式 的m的取值范围为___________。
的m的取值范围为___________。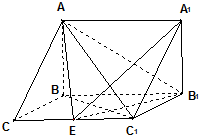 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,CC1=BB1=2,∠BCC1=$\frac{π}{3}$
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,CC1=BB1=2,∠BCC1=$\frac{π}{3}$