题目内容
设{an}是公差为2的等差数列,{bn}是公比为2的等比数列,若a1=b1=1
(1)求{an},{bn}的通项公式;
(2)求数列{anbn}的前n项和Sn.
(1)求{an},{bn}的通项公式;
(2)求数列{anbn}的前n项和Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由条件建立方程组即可求出数列{an}、{bn}的通项公式;
(2)根据错位相减法即可求{anbn}的前n项和Sn.
(2)根据错位相减法即可求{anbn}的前n项和Sn.
解答:
解:(1)设{an}的公差为d=2,{bn}的公比为q=2,
∵a1=b1=1
∴an=1+2(n-1)=2n-1,bn=qn-1=2n-1.
(2)∵anbn=(2n-1)•2n-1,
∴Sn=1×20+3×21+5×22+…+(2n-1)•2n-1,①
2Sn=,1×21+3×22+…+(2n-3)•2n-1+(2n-1)•2n,②
相减得:-Sn=1+2(21+22+…+2n-1)-(2n-1)•2n=2n+1-3-(2n-1)•2n
∴Sn=3+(2n-1)•2n-2n+1=3+(2n-3)•2n
∵a1=b1=1
∴an=1+2(n-1)=2n-1,bn=qn-1=2n-1.
(2)∵anbn=(2n-1)•2n-1,
∴Sn=1×20+3×21+5×22+…+(2n-1)•2n-1,①
2Sn=,1×21+3×22+…+(2n-3)•2n-1+(2n-1)•2n,②
相减得:-Sn=1+2(21+22+…+2n-1)-(2n-1)•2n=2n+1-3-(2n-1)•2n
∴Sn=3+(2n-1)•2n-2n+1=3+(2n-3)•2n
点评:本题主要考查等差数列和等比数列的通项公式的计算,以及利用错位相减法进行求和的内容,考查学生的计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知实数x,y表示的平面区域C:
,则z=2x-y的最大值为( )
|
| A、-1 | B、0 | C、4 | D、5 |
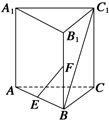 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1的夹角是
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1的夹角是
 如图,DP⊥x轴,点M在DP的延长线上,且
如图,DP⊥x轴,点M在DP的延长线上,且