题目内容
2．已知四面体ABCD的侧面展开图如图所示，则其体积为$\frac{2}{3}$．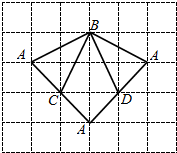
分析 画出展开图的直观图，利用数据求解几何体的体积即可．
解答 
解：将展开图围成一个三棱锥B-ACD如图示，
其中三侧棱均为$\sqrt{5}$，底面是∠A=90°的等腰直角三角形，
且$AC=AD=\sqrt{2}$，∴CD=2，
∵BC=BA=BD，∴B底面射影O为CD中点，
∴AO=1，$BO=\sqrt{5-1}=2$，
${V_{B-ACD}}=\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{2}×2=\frac{2}{3}$．
点评 本题考查几何体的体积的求法，展开图与直观图的关系的判断，考查空间想象能力以及计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．（1）若不等式$sin（2x+\frac{π}{3}）-\frac{1}{a}＞0$对$x∈[\frac{π}{6}，\frac{π}{2}]$的所有实数x都成立，求a的取值范围；
（2）若不等式x2-2ax+2a+1＞0对0≤x≤1的所有实数x都成立，求a的取值范围；
（3）设a＞0且a≠1，f（x）=x2-ax，对x∈（-1，1），均有$f（x）＜\frac{1}{2}$，求a的范围．
（4）完成填空
（2）若不等式x2-2ax+2a+1＞0对0≤x≤1的所有实数x都成立，求a的取值范围；
（3）设a＞0且a≠1，f（x）=x2-ax，对x∈（-1，1），均有$f（x）＜\frac{1}{2}$，求a的范围．
（4）完成填空
| 用图象语言表述 | 用函数最值表述 | |
| 在（a，b）内，若对任意的x有f（x）＞g（x）成立 | ① | ② |
| 在（a，b）内，若存在x0，使f（x）＞g（x）成立 | ③ | ④ |
10．若两条直线ax+2y+6=0与x+（a-1）y+（a2-1）=0平行，则a的取值集合是（ ）
| A． | {-1，2} | B． | {-1} | C． | {2} | D． | $\left\{{\frac{2}{3}}\right\}$ |
17．${（x-\frac{2}{x^2}）^6}$展开式中的常数项为（ ）
| A． | 60 | B． | -60 | C． | 30 | D． | -30 |