题目内容
16.函数f(x)=$\frac{ax+1}{x+2a}$在(-2,2)内为增函数,则a的取值范围是(-∞,-1]∪[1,+∞).分析 将f(x)化简,利用复合函数的单调性列出不等式组解出.
解答 解:f(x)=$\frac{a(x+2a)-2{a}^{2}+1}{x+2a}$=$\frac{1-2{a}^{2}}{x+2a}$+a,∴$\left\{\begin{array}{l}{1-2{a}^{2}<0}\\{-2a≤-2}\end{array}\right.$,或$\left\{\begin{array}{l}{1-2{a}^{2}<0}\\{-2a≥2}\end{array}\right.$,解得a≥1,或a≤-1.
故答案为(-∞,-1]∪[1,+∞).
点评 本题考查了复合函数的单调性,要特别注意函数的定义域.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
4.已知正项等比数列{an}满足a5+a4-a3-a2=8,则a6+a7的最小值为( )
| A. | 4 | B. | 16 | C. | 24 | D. | 32 |
7.某生物产品,每一生产周期成本为10万元,此产品的产量受气候影响、价格受市场影响均具有随机性,且互不影响,其具体情况如表:
(Ⅰ)设X表示1生产周期此产品的利润,求X的分布列;
(Ⅱ)若连续3生产周期,求这3生产周期中至少有2生产周期的利润不少于20万元的概率.
| 产量(吨) | 30 | 50 |
| 概率 | 0.5 | 0.5 |
| 市场价格(万元/吨) | 0.6 | 1 |
| 概率 | 0.4 | 0.6 |
(Ⅱ)若连续3生产周期,求这3生产周期中至少有2生产周期的利润不少于20万元的概率.
8.直线l过圆(x-2)2+(y+2)2=25内一点M(2,2),则l被圆截得的弦长恰为整数的直线共有( )
| A. | 8条 | B. | 7条 | C. | 6条 | D. | 5条 |
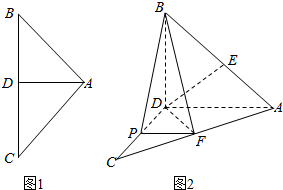 如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证:
如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证: