题目内容
12.已知命题p:方程$\frac{{x}^{2}}{k}$+$\frac{{y}^{2}}{4-k}$=1表示焦点在x轴上的椭圆,命题q:(k-1)x2+(k-3)y2=1表示双曲线.若p∨q为真命题,求实数k的取值范围.分析 分别求出p,q为真时的k的范围,根据若p∨q为真命题,取并集即可.
解答 解:当p为真时,k>4-k>0,即 2<k<4;…(4分)
当q为真时,(k-1)(k-3)<0,即 1<k<3;…(8分)
由题设,p∨q为真命题,
知p和q中至少有一个为真命题,
∴2<k<4或1<k<3,即1<k<4
从而k的取值范围是1<k<4. …(10分)
点评 本题考查了复合命题的判断,考查椭圆和双曲线的性质,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.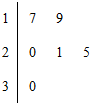 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
( )
 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为 ( )
| A. | $\frac{8}{15}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{9}$ |
7.某生物产品,每一生产周期成本为10万元,此产品的产量受气候影响、价格受市场影响均具有随机性,且互不影响,其具体情况如表:
(Ⅰ)设X表示1生产周期此产品的利润,求X的分布列;
(Ⅱ)若连续3生产周期,求这3生产周期中至少有2生产周期的利润不少于20万元的概率.
| 产量(吨) | 30 | 50 |
| 概率 | 0.5 | 0.5 |
| 市场价格(万元/吨) | 0.6 | 1 |
| 概率 | 0.4 | 0.6 |
(Ⅱ)若连续3生产周期,求这3生产周期中至少有2生产周期的利润不少于20万元的概率.
1.把-1485°转化为α+k•360°(0°≤α<360°,k∈Z)的形式是( )
| A. | 45°-4×360° | B. | -45°-4×360° | C. | -45°-5×360° | D. | 315°-5×360° |
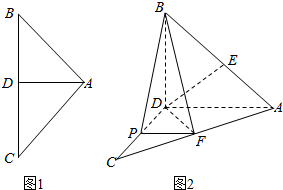 如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证:
如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证: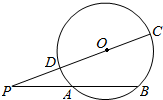 自圆O外一点P引圆O的两条割线PAB和PDC,如图所示,其中割线PDC过圆心O.AB=$\sqrt{2}$OA,PD=$\sqrt{3}$,∠P=15°,
自圆O外一点P引圆O的两条割线PAB和PDC,如图所示,其中割线PDC过圆心O.AB=$\sqrt{2}$OA,PD=$\sqrt{3}$,∠P=15°,