题目内容
17．在$-\frac{π}{4}≤x≤\frac{π}{4}$，则函数y=tanx的值域为[-1，1]．分析 根据正切函数的图象与性质，求出x∈[-$\frac{π}{4}$，$\frac{π}{4}$]时函数y=tanx的值域即可．
解答 解：∵$-\frac{π}{4}≤x≤\frac{π}{4}$，
∴-1≤tanx≤1，
∴函数y=tanx的值域为[-1，1]．
故答案为：[-1，1]．
点评 本题考查了正切函数的图象与性质的应用问题，是基础题目．
练习册系列答案
名校课堂系列答案
相关题目
7．某生物产品，每一生产周期成本为10万元，此产品的产量受气候影响、价格受市场影响均具有随机性，且互不影响，其具体情况如表：
（Ⅰ）设X表示1生产周期此产品的利润，求X的分布列；
（Ⅱ）若连续3生产周期，求这3生产周期中至少有2生产周期的利润不少于20万元的概率．
| 产量（吨） | 30 | 50 |
| 概率 | 0.5 | 0.5 |
| 市场价格（万元/吨） | 0.6 | 1 |
| 概率 | 0.4 | 0.6 |
（Ⅱ）若连续3生产周期，求这3生产周期中至少有2生产周期的利润不少于20万元的概率．
8．直线l过圆（x-2）2+（y+2）2=25内一点M（2，2），则l被圆截得的弦长恰为整数的直线共有（ ）
| A． | 8条 | B． | 7条 | C． | 6条 | D． | 5条 |
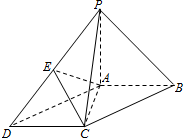如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且AB=AC=$\frac{1}{2}$PA=1，点E是PD的中点．
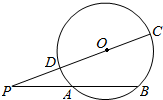自圆O外一点P引圆O的两条割线PAB和PDC，如图所示，其中割线PDC过圆心O．AB=$\sqrt{2}$OA，PD=$\sqrt{3}$，∠P=15°，