题目内容
16.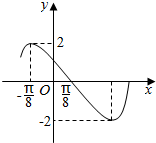 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,则函数的解析式为( )
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,则函数的解析式为( )| A. | y=2sin(2x-$\frac{π}{4}$) | B. | y=2sin(2x-$\frac{π}{4}$)或y=2sin(2x+$\frac{3π}{4}$) | ||
| C. | y=2sin(2x+$\frac{3π}{4}$) | D. | y=2sin(2x-$\frac{3π}{4}$) |
分析 根据函数振幅求得A;根据周期求得w;根据f($\frac{π}{8}$)=0求得φ,即可得解.
解答 解:由图象可知函数振幅为2,故A=2,
周期为4×($\frac{π}{8}$+$\frac{π}{8}$)=π,故w=$\frac{2π}{π}$=2,
f($\frac{π}{8}$)=2sin(2×$\frac{π}{8}$+φ)=0,且|φ|<π,故φ=$\frac{3π}{4}$.
故函数的解析式为:y=2sin(2x+$\frac{3π}{4}$).
故选:C.
点评 本题主要考查函数y=Asin(ωx+φ)部分图象确定函数解析式.属基础题.

练习册系列答案
相关题目
4.已知正项等比数列{an}满足a5+a4-a3-a2=8,则a6+a7的最小值为( )
| A. | 4 | B. | 16 | C. | 24 | D. | 32 |
7.某生物产品,每一生产周期成本为10万元,此产品的产量受气候影响、价格受市场影响均具有随机性,且互不影响,其具体情况如表:
(Ⅰ)设X表示1生产周期此产品的利润,求X的分布列;
(Ⅱ)若连续3生产周期,求这3生产周期中至少有2生产周期的利润不少于20万元的概率.
| 产量(吨) | 30 | 50 |
| 概率 | 0.5 | 0.5 |
| 市场价格(万元/吨) | 0.6 | 1 |
| 概率 | 0.4 | 0.6 |
(Ⅱ)若连续3生产周期,求这3生产周期中至少有2生产周期的利润不少于20万元的概率.
1.把-1485°转化为α+k•360°(0°≤α<360°,k∈Z)的形式是( )
| A. | 45°-4×360° | B. | -45°-4×360° | C. | -45°-5×360° | D. | 315°-5×360° |
8.直线l过圆(x-2)2+(y+2)2=25内一点M(2,2),则l被圆截得的弦长恰为整数的直线共有( )
| A. | 8条 | B. | 7条 | C. | 6条 | D. | 5条 |
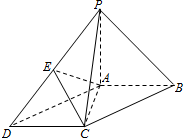 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.