题目内容
15.已知函数f(x)=ax2+bx+c,a,b,c∈R,且a≠0.记M(a,b,c)为|f(x)|在[0,1]上的最大值,则$\frac{a+b+2c}{M(a,b,c)}$的最大值是2.分析 先求出a+b+2c=f(0)+f(1),判断出f(0)+f(1)>0,通过讨论f(0),f(1),M(a,b,c)的大小,从而求出代数式的最大值即可.
解答 解:a+b+2c=f(0)+f(1),为取得最大值,
显然此表达式可取正值,不需要考虑负值的情况,
∴f(0)+f(1)>0,
在x∈[0,1]上,最大的值可能为f(0),f(1),M(a,b,c)中的任何一个,
①若f(0)或f(1)取最大时,不妨设f(1)<f(0)最大,
则M(a,b,c)=f(0),$\frac{f(0)+f(1)}{M(a,b,c)}$<2,
②若f(0)=f(1),同时取最大,
则M(a,b,c)=f(0),$\frac{f(0)+f(1)}{M(a,b,c)}$=2,
③若M(a,b,c)取最大,
则f(0)<M(a,b,c),f(1)<M(a,b,c),
$\frac{f(0)+f(1)}{M(a,b,c)}$<2,
∴最大值为2,
故答案为:2.
点评 本题考查了二次函数的性质,考查分类讨论思想,是一道中档题.

练习册系列答案
相关题目
4.已知正项等比数列{an}满足a5+a4-a3-a2=8,则a6+a7的最小值为( )
| A. | 4 | B. | 16 | C. | 24 | D. | 32 |
20.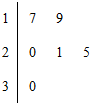 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
( )
 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为 ( )
| A. | $\frac{8}{15}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{9}$ |
7.某生物产品,每一生产周期成本为10万元,此产品的产量受气候影响、价格受市场影响均具有随机性,且互不影响,其具体情况如表:
(Ⅰ)设X表示1生产周期此产品的利润,求X的分布列;
(Ⅱ)若连续3生产周期,求这3生产周期中至少有2生产周期的利润不少于20万元的概率.
| 产量(吨) | 30 | 50 |
| 概率 | 0.5 | 0.5 |
| 市场价格(万元/吨) | 0.6 | 1 |
| 概率 | 0.4 | 0.6 |
(Ⅱ)若连续3生产周期,求这3生产周期中至少有2生产周期的利润不少于20万元的概率.
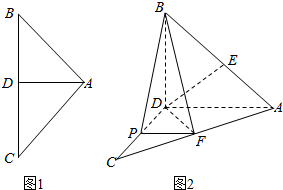 如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证:
如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证: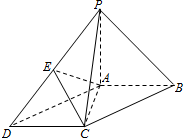 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.