题目内容
设M={x|0≤x≤2}，N={y|0≤y≤2}，给出下列四个图形，其中能表示集合M到集合N的映射关系的有（ ）
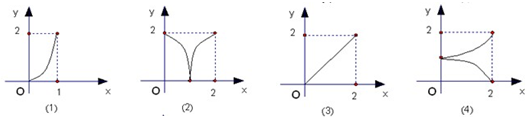
| A、0个 | B、1个 | C、2个 | D、3个 |
考点：映射
专题：阅读型
分析：由映射概念逐一核对四个图象即可得到答案．
解答：
解：图象（1）中，集合M内（1，2]的元素在集合N内没有对应元素，∴图象（1）不能表示集合M到集合N的映射；
图象（2）中，集合M内的任意元素在集合N中都有唯一确定的对应元素，∴图象（2）能表示集合M到集合N的映射；
图象（3）中，集合M内的任意元素在集合N中都有唯一确定的对应元素，∴图象（3）能表示集合M到集合N的映射；
图象（4）中，集合M内的元素在集合N中对应的元素不唯一，∴图象（4）不能表示集合M到集合N的映射．
∴能表示集合M到集合N的映射关系的是（2）、（3）．
故选：C．
图象（2）中，集合M内的任意元素在集合N中都有唯一确定的对应元素，∴图象（2）能表示集合M到集合N的映射；
图象（3）中，集合M内的任意元素在集合N中都有唯一确定的对应元素，∴图象（3）能表示集合M到集合N的映射；
图象（4）中，集合M内的元素在集合N中对应的元素不唯一，∴图象（4）不能表示集合M到集合N的映射．
∴能表示集合M到集合N的映射关系的是（2）、（3）．
故选：C．
点评：本题考查了映射概念，解答的关键是对映射概念的理解，是基础的概念题．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
圆（x-1）2+（y+1）2=2的周长是（ ）
A、
| ||
| B、2π | ||
C、2
| ||
| D、4π |
已知集合M={-2，2}，N={x|ax-2=0}，若N⊆M，则由实数a的所有可能值构成的集合为（ ）
| A、{-1} |
| B、{1} |
| C、{-1，1} |
| D、{-1，0，1} |
已知函数y=f（n），满足f（1）=8，且f（n+1）=f（n）+7，n∈N+．则f（3）=（ ）
| A、7 | B、15 | C、22 | D、28 |
命题p：不等式|
|＞
的解集为{x|0＜x＜1}；命题q：0＜a≤
是函数f（x）=ax2+2（a-1）x+2在区间（-∞，4]上为减函数的充分不必要条件，则（ ）
| x |
| x-1 |
| x |
| x-1 |
| 1 |
| 5 |
| A、p真q假 |
| B、“p且q”为真 |
| C、“p或q”为假 |
| D、p假q真 |
在圆x2+y2=4上任取一点P，过点P作x轴的垂线段PD，D为垂足．当点P在圆上运动时，线段PD的中点M的轨迹是（ ）
| A、椭圆 | B、双曲线 | C、抛物线 | D、圆 |