题目内容
设集合A={x|x2-3x-10≤0},B={x|(x-m+1)(x-2m-1)<0}.
(1)求A∩Z;
(2)若A∪B=A,求m的取值范围.
(1)求A∩Z;
(2)若A∪B=A,求m的取值范围.
考点:集合的包含关系判断及应用
专题:不等式的解法及应用,集合
分析:(1)把集合A、B化简,由两集合的交集即可得到A∩Z;
(2)在(1)化简后的基础上,借助于子集概念得到两集合端点值的关系,求解不等式得到m的范围.
(2)在(1)化简后的基础上,借助于子集概念得到两集合端点值的关系,求解不等式得到m的范围.
解答:
解:(Ⅰ)化简可得,集合A={x|-2≤x≤5}
则A∩Z={-2,-1,0,1,2,3,4,5}.
(Ⅱ)由A∪B=A,知B⊆A
集合B={x|(x-m+1)(x-2m-1)<0},
①当m=-2时,B=∅,所以B⊆A;
②当m<-2时,
∵(2m+1)-(m-1)=2+m<0,
∴B=(2m+1,m-1).
因此,要使B⊆A,只需
,解得-
≤m≤6,
所以m值不存在.
③当m>-2时,B=(m-1,2m+1),
要使B⊆A,只需
,-1≤m≤2.
综上所述,m的取值范围是m=-2或-1≤m≤2
则A∩Z={-2,-1,0,1,2,3,4,5}.
(Ⅱ)由A∪B=A,知B⊆A
集合B={x|(x-m+1)(x-2m-1)<0},
①当m=-2时,B=∅,所以B⊆A;
②当m<-2时,
∵(2m+1)-(m-1)=2+m<0,
∴B=(2m+1,m-1).
因此,要使B⊆A,只需
|
| 3 |
| 2 |
所以m值不存在.
③当m>-2时,B=(m-1,2m+1),
要使B⊆A,只需
|
综上所述,m的取值范围是m=-2或-1≤m≤2
点评:本题考查了交集及其运算,考查了不等式的解法,是中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
设向量
,
,
满足
+
+
=
,且
⊥
,|
|=1,|
|=2,则|
|2=( )
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| a |
| b |
| c |
| A、1 | B、2 | C、3 | D、5 |
设M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形,其中能表示集合M到集合N的映射关系的有( )
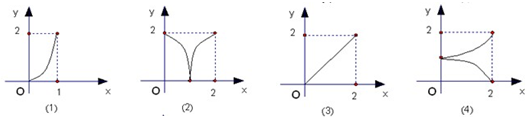

| A、0个 | B、1个 | C、2个 | D、3个 |