题目内容
命题p：不等式|
|＞
的解集为{x|0＜x＜1}；命题q：0＜a≤
是函数f（x）=ax2+2（a-1）x+2在区间（-∞，4]上为减函数的充分不必要条件，则（ ）
| x |
| x-1 |
| x |
| x-1 |
| 1 |
| 5 |
| A、p真q假 |
| B、“p且q”为真 |
| C、“p或q”为假 |
| D、p假q真 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：分别判断命题p，q的真假性，然后根据复合命题之间的关系进行判断即可．
解答：
解：若不等式|
|＞
成立，则不等式
＜0，即0＜x＜1，∴命题p为真命题．
若函数f（x）=ax2+2（a-1）x+2在区间（-∞，4]上为减函数，
则当a=0时，函数f（x）=-2x+2，满足条件．
当a≠0，要使函数f（x）=ax2+2（a-1）x+2在区间（-∞，4]上为减函数，
则
，
∴
，
即0＜a≤
，
综上0≤a≤
，
∴0＜a≤
是函数f（x）=ax2+2（a-1）x+2在区间（-∞，4]上为减函数的充分不必要条件，
∴命题q是真命题．
∴“p且q”为真，
故选：B．
| x |
| x-1 |
| x |
| x-1 |
| x |
| x-1 |
若函数f（x）=ax2+2（a-1）x+2在区间（-∞，4]上为减函数，
则当a=0时，函数f（x）=-2x+2，满足条件．
当a≠0，要使函数f（x）=ax2+2（a-1）x+2在区间（-∞，4]上为减函数，
则
|
∴
|
即0＜a≤
| 1 |
| 5 |
综上0≤a≤
| 1 |
| 5 |
∴0＜a≤
| 1 |
| 5 |
∴命题q是真命题．
∴“p且q”为真，
故选：B．
点评：本题主要考查复合命题与简单命题之间的关系，利用条件判断命题p，q的真假是解决本题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
如果命题“p或q”为真命题，则（ ）
| A、p，q均为真命题 |
| B、p，q均为假命题 |
| C、￢p，￢q中至少有一个为假命题 |
| D、￢p，￢q中至多有一个为假命题 |
在平面直角坐标系xoy中不等式组
确定的平面区域为D，在区域D中任取一点P（a，b），则P满足a+2b＞10的概率为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
设M={x|0≤x≤2}，N={y|0≤y≤2}，给出下列四个图形，其中能表示集合M到集合N的映射关系的有（ ）
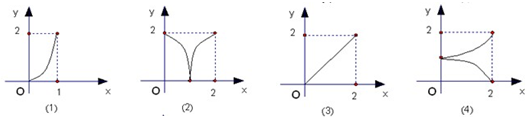
| A、0个 | B、1个 | C、2个 | D、3个 |
已知不等式ax2-bx+1≥0的解集是[-1，2]，则不等式x2-bx+a＜0的解集是（ ）
A、（-
| ||
B、（-∞，-1）∪（
| ||
C、（-∞，-
| ||
D、（-1，
|