题目内容
已知集合M={-2，2}，N={x|ax-2=0}，若N⊆M，则由实数a的所有可能值构成的集合为（ ）
| A、{-1} |
| B、{1} |
| C、{-1，1} |
| D、{-1，0，1} |
考点：集合的包含关系判断及应用
专题：集合
分析：本题首先认清集合N的元素，带入方程ax-2=0，求解a即可．
解答：
解：∵N⊆M，M={-2，2}，N={x|ax-2=0}
∴N=Φ或N={-2}或N={2}
∴a=0，-1，1
故选D
∴N=Φ或N={-2}或N={2}
∴a=0，-1，1
故选D
点评：本题属于以一元一次方程为依托，求集合的相等关系的基础题，也是高考常会考的题型．
练习册系列答案
相关题目
设向量
，
，
满足
+
+
=
，且
⊥
，|
|=1，|
|=2，则|
|2=（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| a |
| b |
| c |
| A、1 | B、2 | C、3 | D、5 |
如果命题“p或q”为真命题，则（ ）
| A、p，q均为真命题 |
| B、p，q均为假命题 |
| C、￢p，￢q中至少有一个为假命题 |
| D、￢p，￢q中至多有一个为假命题 |
曲线y=
ex在点(2，
e2)处的切线与坐标轴所围三角形的面积为（ ）
| 1 |
| 2 |
| 1 |
| 2 |
A、
| ||
| B、4e2 | ||
| C、2e2 | ||
D、
|
在平面直角坐标系xoy中不等式组
确定的平面区域为D，在区域D中任取一点P（a，b），则P满足a+2b＞10的概率为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
设M={x|0≤x≤2}，N={y|0≤y≤2}，给出下列四个图形，其中能表示集合M到集合N的映射关系的有（ ）
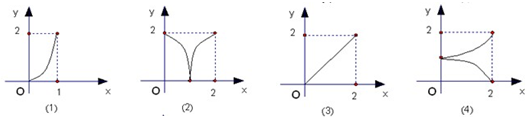
| A、0个 | B、1个 | C、2个 | D、3个 |