题目内容
已知函数y=f（n），满足f（1）=8，且f（n+1）=f（n）+7，n∈N+．则f（3）=（ ）
| A、7 | B、15 | C、22 | D、28 |
考点：函数的值
专题：函数的性质及应用
分析：由题设条件，利用递推思想能求出f（3）．
解答：
解：∵f（1）=8，且f（n+1）=f（n）+7，n∈N+，
∴f（2）=f（1）+7=8+7=15，
f（3）=15+7=22．
故选：C．
∴f（2）=f（1）+7=8+7=15，
f（3）=15+7=22．
故选：C．
点评：本题考查函数值的求法，解题时要认真审题，注意递推思想的合理运用．
练习册系列答案
考前必练系列答案
相关题目
设A={-4，2a-1，a2}，B={9，a-5，1-a}，已知A∩B={9}，则实数a的值为（ ）
| A、5 | B、±3 | C、-3 | D、3 |
曲线y=
ex在点(2，
e2)处的切线与坐标轴所围三角形的面积为（ ）
| 1 |
| 2 |
| 1 |
| 2 |
A、
| ||
| B、4e2 | ||
| C、2e2 | ||
D、
|
已知A（-2，-2），B（4，2），点P在圆x2+y2=1上运动，则|PA|2+|PB|2的最大值是（ ）
| A、28 | B、30 | C、32 | D、34 |
设M={x|0≤x≤2}，N={y|0≤y≤2}，给出下列四个图形，其中能表示集合M到集合N的映射关系的有（ ）
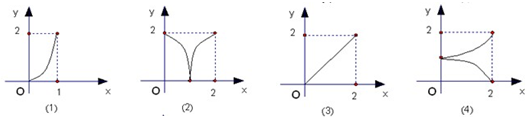
| A、0个 | B、1个 | C、2个 | D、3个 |
圆心是O（-3，4），半径长为5的圆的方程是（ ）
| A、（x-3）2+（y+4）2=5 |
| B、（x-3）2+（y+4）2=25 |
| C、（x+3）2+（y-4）2=5 |
| D、（x+3）2+（y-4）2=25 |