题目内容
圆（x-1）2+（y+1）2=2的周长是（ ）
A、
| ||
| B、2π | ||
C、2
| ||
| D、4π |
考点：圆的标准方程
专题：直线与圆
分析：根据圆的标准方程可得圆的半径为r=
，用圆的周长公式即得．
| 2 |
解答：
解：由圆的方程（x-1）2+（y+1）2=2，
得圆的半径r=
．
由圆的周长公式，得
圆的周长l=2πr=2
π．
故选C．
得圆的半径r=
| 2 |
由圆的周长公式，得
圆的周长l=2πr=2
| 2 |
故选C．
点评：本题考查圆的周长公式，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
设向量
，
，
满足
+
+
=
，且
⊥
，|
|=1，|
|=2，则|
|2=（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| a |
| b |
| c |
| A、1 | B、2 | C、3 | D、5 |
设A={-4，2a-1，a2}，B={9，a-5，1-a}，已知A∩B={9}，则实数a的值为（ ）
| A、5 | B、±3 | C、-3 | D、3 |
如果命题“p或q”为真命题，则（ ）
| A、p，q均为真命题 |
| B、p，q均为假命题 |
| C、￢p，￢q中至少有一个为假命题 |
| D、￢p，￢q中至多有一个为假命题 |
曲线y=
ex在点(2，
e2)处的切线与坐标轴所围三角形的面积为（ ）
| 1 |
| 2 |
| 1 |
| 2 |
A、
| ||
| B、4e2 | ||
| C、2e2 | ||
D、
|
设M={x|0≤x≤2}，N={y|0≤y≤2}，给出下列四个图形，其中能表示集合M到集合N的映射关系的有（ ）
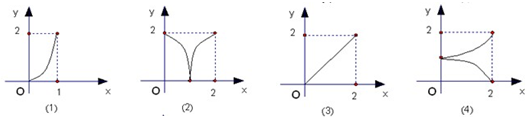
| A、0个 | B、1个 | C、2个 | D、3个 |