题目内容
在圆x2+y2=4上任取一点P，过点P作x轴的垂线段PD，D为垂足．当点P在圆上运动时，线段PD的中点M的轨迹是（ ）
| A、椭圆 | B、双曲线 | C、抛物线 | D、圆 |
考点：轨迹方程
专题：圆锥曲线的定义、性质与方程
分析：设出M点的坐标，由M为线段PD的中点得到P的坐标，把P的坐标代入圆x2+y2=4整理得线段PD的中点M的轨迹．
解答：
解：设M（x，y），由题意D（x，0），P（x，y1）
∵M为线段PD的中点，∴y1+0=2y，y1=2y．
又∵P（x，y1）在圆x2+y2=4上，∴x2+y12=4，
∴x2+4y2=4，即
+y2=1．
∴点M的轨迹方程为
+y2=1．
故选：A．
∵M为线段PD的中点，∴y1+0=2y，y1=2y．
又∵P（x，y1）在圆x2+y2=4上，∴x2+y12=4，
∴x2+4y2=4，即
| x2 |
| 4 |
∴点M的轨迹方程为
| x2 |
| 4 |
故选：A．
点评：本题考查了轨迹方程的求法，训练了利用代入法求曲线的方程，是中档题．
练习册系列答案
全优点练单元计划系列答案
相关题目
曲线y=
ex在点(2，
e2)处的切线与坐标轴所围三角形的面积为（ ）
| 1 |
| 2 |
| 1 |
| 2 |
A、
| ||
| B、4e2 | ||
| C、2e2 | ||
D、
|
设M={x|0≤x≤2}，N={y|0≤y≤2}，给出下列四个图形，其中能表示集合M到集合N的映射关系的有（ ）
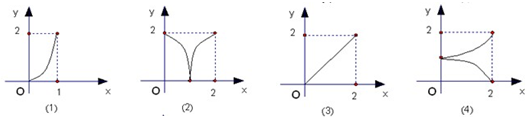
| A、0个 | B、1个 | C、2个 | D、3个 |
圆心是O（-3，4），半径长为5的圆的方程是（ ）
| A、（x-3）2+（y+4）2=5 |
| B、（x-3）2+（y+4）2=25 |
| C、（x+3）2+（y-4）2=5 |
| D、（x+3）2+（y-4）2=25 |