题目内容
若α=k•180°+45°,k∈Z,则α为 象限角.
考点:象限角、轴线角
专题:三角函数的图像与性质
分析:直接分k为偶数和奇数讨论,由k为偶数和奇数首先确定k•180°的终边,加上45°可得答案.
解答:
解:由α=k•180°+45°(k∈Z),
当k=2n为偶数时,k•180°=n•360°的终边位于x轴正半轴,则α=k•180°+45°(k∈Z)为第一象限角;
当k=2n+1为奇数时,k•180°=n•360°+180°的终边位于x轴负半轴,则α=k•180°+45°(k∈Z)为第三象限角.
所以α的终边在第一或第三象限.
故答案为:第一或第三.
当k=2n为偶数时,k•180°=n•360°的终边位于x轴正半轴,则α=k•180°+45°(k∈Z)为第一象限角;
当k=2n+1为奇数时,k•180°=n•360°+180°的终边位于x轴负半轴,则α=k•180°+45°(k∈Z)为第三象限角.
所以α的终边在第一或第三象限.
故答案为:第一或第三.
点评:本题考查了象限角和轴线角,是基础的概念题,属会考题型.

练习册系列答案
相关题目
设向量
,
,
满足
+
+
=
,且
⊥
,|
|=1,|
|=2,则|
|2=( )
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| a |
| b |
| c |
| A、1 | B、2 | C、3 | D、5 |
设M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形,其中能表示集合M到集合N的映射关系的有( )
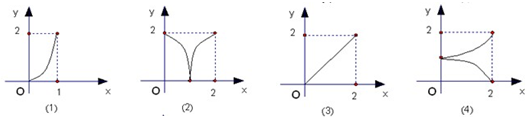

| A、0个 | B、1个 | C、2个 | D、3个 |