题目内容
16.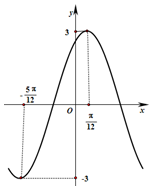 函数y=Asin(ω•x+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为y=3sin(2x+$\frac{π}{3}$).
函数y=Asin(ω•x+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为y=3sin(2x+$\frac{π}{3}$).
分析 根据图中数据,求出A,ω和φ的值即可写出函数的解析式.
解答 解:由图象知A=3,且$\frac{1}{2}$T=$\frac{π}{12}$-(-$\frac{5π}{12}$)=$\frac{π}{2}$,
解得T=π;
即$\frac{2π}{ω}$=π,解得ω=2,
则y=3sin(2x+φ),
所以当x=$\frac{π}{12}$时,y=3sin(2×$\frac{π}{12}$+φ)=3,
即sin($\frac{π}{6}$+φ)=1,
解得$\frac{π}{6}$+φ=2kπ+$\frac{π}{2}$,即φ=2kπ+$\frac{π}{3}$,
∵|φ|<π,
∴当k=0时,φ=$\frac{π}{3}$,
即y=3sin(2x+$\frac{π}{3}$).
故答案为:y=3sin(2x+$\frac{π}{3}$).
点评 本题主要考查了求三角函数解析式问题,是基础题目.

练习册系列答案
相关题目
7.已知集合M={x|(x+2)(x-2)>0},N={-3,-2,2,3,4},则M∩N=( )
| A. | {3,4} | B. | {-3,3,4} | C. | {-2,3,4} | D. | {-3,-2,2,3,4} |
11.已知0≤x≤$\frac{3}{2}$,则函数f(x)=x2+x+1( )
| A. | 有最小值-$\frac{3}{4}$,无最大值 | B. | 有最小值$\frac{3}{4}$,最大值1 | ||
| C. | 有最小值1,最大值$\frac{19}{4}$ | D. | 无最小值和最大值 |
8.在空间直角坐标系中,已知点A(1,0,2),B(1,-4,0),点M是A,B的中点,则点M的坐标是( )
| A. | (1,-1,0) | B. | (1,-2,1) | C. | (2,-4,2) | D. | (1,-4,1) |