题目内容
10.在平面直角坐标系中,已知角α的终边经过点P(-3,4)(1)求sinα和cosα的值;
(2)求$tan(α+\frac{π}{4})$的值;
(3)求${sin^2}(α+\frac{π}{4})+sin(α+\frac{π}{4})•cos(α+\frac{π}{4})$的值.
分析 (1)由题意和三角函数的定义求出sinα和cosα的值;
(2)由题意和正切函数的定义求出tanα,由两角和的正切公式求出答案;
(3)由平方关系将分式化为齐次时,由商的关系化简正切,将(2)中的值代入求值即可.
解答 解(1)由题意知,x=-3,y=4,则r=5,
∴$sinα=\frac{y}{r}=\frac{4}{5},cosα=\frac{x}{r}=-\frac{3}{5}$;…(3分)
(2)∵角α的终边经过点P(-3,4),
∴$tanα=-\frac{4}{3}$,
∴$tan(α+\frac{π}{4})=\frac{1+tanα}{1-tanα}=-\frac{1}{7}$;…(6分)
(3)原式=$\frac{{sin}^{2}(α+\frac{π}{4})+sin(α+\frac{π}{4})•cos(α+\frac{π}{4})}{{sin}^{2}(α+\frac{π}{4})+{cos}^{2}(α+\frac{π}{4})}$
=$\frac{{tan}^{2}(α+\frac{π}{4})+tan(α+\frac{π}{4})}{{tan}^{2}(α+\frac{π}{4})+1}=\frac{\frac{1}{49}-\frac{1}{7}}{\frac{1}{49}+1}=-\frac{3}{25}$…(10分)
点评 本题考查两角和的正切公式,三角函数的定义,及同角三角函数的基本关系的应用,考查化简、变形能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
18.设集合M={x|x2=x},N={x|1<2x<2},则M∪N=( )
| A. | (-∞,2] | B. | (0,1] | C. | (0,2] | D. | [0,1] |
2.下列表格所示的五个散点,原本数据完整,且利用最小二乘法求得这五个散点的线性回归直线方程为$\stackrel{∧}{y}$=0.8x+155,后因某未知原因第5组数据的y值模糊不清,此位置数据记为m(如表所示),则利用回归方程可求得实数m的值为( )
| x | 196 | 197 | 200 | 203 | 204 |
| y | 1 | 3 | 6 | 7 | m |
| A. | 8.3 | B. | 8.2 | C. | 8.1 | D. | 8 |
19.某校高三文科600名学生参加了12月的模拟考试,学校为了了解高三文科学生的数学、外语情况,利用随机数表法从中抽取100名学生的成绩进行统计分析,抽出的100名学生的数学、外语成绩如表:
(Ⅰ)若数学成绩优秀率为35%,求m,n的值;
(Ⅱ)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
| 外语 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 8 | m | 9 |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
(Ⅱ)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
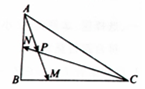 在△ABC中,$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$
在△ABC中,$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$