题目内容
5.定义在(0,+∞)上的单调函数f(x),对任意x∈(0,+∞),f[f(x)-log2x]=3成立,若方程f(x)-f'(x)=2的解在区间(k,k+1)(k∈Z)内,则k=1.分析 设t=f(x)-log2x,则f(x)=log2x+t,又由f(t)=3,即log2t+t=3,解可得t的值,可得f(x)的解析式,由二分法分析可得h(x)的零点所在的区间为(1,2),结合函数的零点与方程的根的关系,即可得答案.
解答 解:根据题意,对任意的x∈(0,+∞),都有f[f(x)-log2x]=3,
又由f(x)是定义在(0,+∞)上的单调函数,
则f(x)-log2x为定值,
设t=f(x)-log2x,则f(x)=log2x+t,
又由f(t)=3,即log2t+t=3,
解可得,t=2;
则f(x)=log2x+2,f′(x)=$\frac{1}{ln2•x}$,
将f(x)=log2x+2,f′(x)=$\frac{1}{xln2}$代入f(x)-f′(x)=2,
可得log2x+2-$\frac{1}{xln2}$=2,
即log2x-$\frac{1}{xln2}$=0,
令h(x)=log2x-$\frac{1}{xln2}$,
分析易得h(1)=$\frac{1}{ln2}$<0,h(2)=1-$\frac{1}{2ln2}$>0,
则h(x)=log2x-$\frac{1}{xln2}$的零点在(1,2)之间,
则方程log2x-$\frac{1}{xln2}$=0,即f(x)-f′(x)=2的根在(1,2)上,
故答案为:1.
点评 本题考查二分法求函数的零点与函数零点与方程根的关系的应用,关键点和难点是求出f(x)的解析式.

练习册系列答案
相关题目
8.$\root{3}{(lg50-1)^{3}}$-$\sqrt{(lg2-1)^{2}}$=( )
| A. | 2lg5 | B. | 0 | C. | -1 | D. | -2lg5 |
16.若函数$f(x)=sin(\frac{1}{2}x+\frac{π}{6})$,则f(x)( )
| A. | 图象关于$x=\frac{π}{3}$对称 | |
| B. | 图象关于$(\frac{2π}{3},0)$对称 | |
| C. | 在$[\frac{2π}{3},\frac{8π}{3}]$上单调递减 | |
| D. | 单调递增区间是$[2kπ-\frac{4π}{3},2kπ+\frac{2π}{3}](k∈Z)$ |
13.已知i为虚数单位,则$\frac{1-i}{i^3}$=( )
| A. | 1+i | B. | 1-i | C. | -1-i | D. | -1+i |
15.两条直线l1:ax+(1+a)y=3,l2:(a+1)x+(3-2a)y=2互相垂直,则a的值是 ( )
| A. | 3 | B. | -1 | C. | -1或3 | D. | 0 或 3 |
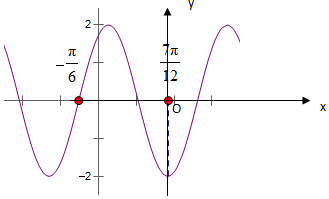 已知f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象如图所示.
已知f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象如图所示.