题目内容
2.下列表格所示的五个散点,原本数据完整,且利用最小二乘法求得这五个散点的线性回归直线方程为$\stackrel{∧}{y}$=0.8x+155,后因某未知原因第5组数据的y值模糊不清,此位置数据记为m(如表所示),则利用回归方程可求得实数m的值为( )| x | 196 | 197 | 200 | 203 | 204 |
| y | 1 | 3 | 6 | 7 | m |
| A. | 8.3 | B. | 8.2 | C. | 8.1 | D. | 8 |
分析 根据回归直线经过样本数据中心点,求出x、y的平均数,即可求出m值.
解答 解:根据题意,计算 $\overline{x}$=$\frac{1}{5}$×(196+197+200+203+204)=200,
$\overline{y}$=$\frac{1}{5}$×(1+3+6+7+m)=$\frac{17+m}{5}$,
代入回归方程$\stackrel{∧}{y}$=0.8x-155中,
可得$\frac{17+m}{5}$=0.8×200-155=25,
解得m=8.
故选:D
点评 本题考查了线性回归方程过样本中心点的应用问题,是基础题目.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
13.已知i为虚数单位,则$\frac{1-i}{i^3}$=( )
| A. | 1+i | B. | 1-i | C. | -1-i | D. | -1+i |
11.若全集U={0,1,2,3},A={0,1,2},B={0,2,3},则A∪(∁UB)=( )
| A. | ∅ | B. | {1} | C. | {0,1,2} | D. | {2,3} |
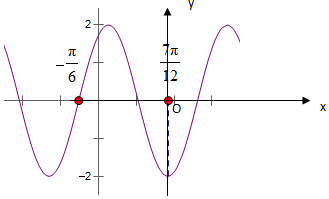 已知f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象如图所示.
已知f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象如图所示.