题目内容
15.若对于任意正数x,y,都有f(xy)=f(x)+f(y),且f(8)=-3,则$f(a)=\frac{1}{2}$时,正数a=$\frac{\sqrt{2}}{2}$.分析 分别赋值,即可求出答案.
解答 解:f(8)=f(2×4)=f(2)+f(4)=f(2)+f(2)+f(2)=3f(2)=-3,
∴f(2)=-1,
∴f(2)=2f($\sqrt{2}$)=-1,
∴f($\sqrt{2}$)=-$\frac{1}{2}$,
∴f($\sqrt{2}$)=f($\frac{\sqrt{2}}{2}$×2)=f($\frac{\sqrt{2}}{2}$)+f(2)=-$\frac{1}{2}$,
∴f($\frac{\sqrt{2}}{2}$)=$\frac{1}{2}$.
∴a=$\frac{{\sqrt{2}}}{2}$,
故答案为:$\frac{{\sqrt{2}}}{2}$.
点评 本题考查了抽象函数的问题,关键是赋值,属于基础题.

练习册系列答案
相关题目
6.已知f(x)为偶函数,且f(x)=f(x-4),在区间[0,2]上,f(x)=$\left\{\begin{array}{l}{-{x}^{2}-\frac{3}{2}x+5,0≤x≤1}\\{{2}^{x}+{2}^{-x},a<x≤2}\end{array}\right.$,g(x)=($\frac{1}{2}$)|x|+a,若F(x)=f(x)-g(x)恰好有4个零点,则a的取值范围是( )
| A. | (2,$\frac{19}{8}$) | B. | (2,3) | C. | (2,$\frac{19}{8}$] | D. | (2,3] |
3.已知函数f(x)=x3+x-1,则在下列区间中,f(x)一定有零点的是( )
| A. | (-1,0) | B. | (0,1) | C. | (-2,-1) | D. | (1,2) |
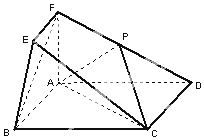 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=l,点P在棱DF上.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=l,点P在棱DF上.