题目内容

|
a
|=1，|
b
|=2，
a
•（
a
-2
b
）=0，则|
a
-
b
|=（　　）
A、2B、4C、1D、8
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：根据数量积的运算及已知条件可求出
a
•
b
，这样即可求出(
a
-
b
)2，所以便可求得|
a
-
b
|=
(
a
-
b
)2
．
解答： 解：由
a
•(
a
-2
b
)=0得：
a
2-2
a
•
b
=1-2
a
•
b
=0，
∴
a
•
b
=
1
2
；
∴|
a
-
b
|=
(
a
-
b
)2
=
a
2-2
a
•
b
+
b
2
=
1-1+4
=2．
故选A．
点评：考查数量积的运算，求向量长度的方法：对向量的平方进行开方．
练习册系列答案
相关题目
在等比数列{an}中，若a2a3a6a9a10=32，则
(a10)2
a14
的值为（　　）
A、4B、2C、-2D、-4
设函数f（x）=
2x，．x∈(-∞，2]
log2x，x∈(2，+∞)
，则满足f（x）=4的x的值是（　　）
A、2B、16
C、2或16D、-2或16
设tanα=3，则
sin(α-π)+cos(π-α)
sin(
π
2
-α)+cos(
π
2
+α)
=（　　）
A、3B、2C、1D、-1
已知点（a，2）（a＞0）到直线l：x-y+3=0的距离为
2
，则a=（　　）
A、
2
或-
2
B、1或-3
C、
2-1
D、
2+1
已知在等差数列{an}中，a2=2，a6=6，在等比数列{bn}中，b3=4，b4=8，
（1）求an及bn；
（2）设数列{an•bn}的前n项和Sn，求S5．
已知函数f（x）=3x3-x+1．
（1）求函数f（x）的单调递减区间；
（2）求切于点（1，3）的切线方程；
（3）求函数f（x）在[-1，
1
3
]上的最大值与最小值．
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的图象上相邻的最高点与最低点的坐标分别为（
5π
12
，3）和（
11π
12
，-3），
求（1）求该函数的解析式
（2）若关于x的方程f（x）=a在（0，
7π
6
）有两个不同的实数根，求a的取值范围．
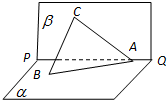已知直二面角α-PQ-β，A∈PQ，B∈α，C∈β，CA=CB，∠BAP=45°，直线CA和平面α所成的角为30°．
（1）求证：BC⊥PQ；    
（2）若AC=2，求二面角B-AC-P的正切值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网