题目内容
11.不等式$\frac{2-x}{1+x}$≥0的解集为( )| A. | (-1,2] | B. | [-1,2] | C. | (-∞,-1)∪(2,+∞) | D. | (-∞,-1]∪(2,+∞) |
分析 要求的不等式等价于$\left\{\begin{array}{l}{x+1≠0}\\{(x-2)(x+1)≤0}\end{array}\right.$,由此求得不等式的解集.
解答 解:不等式$\frac{2-x}{1+x}$≥0等价于$\frac{x-2}{x+1}$≤0,即$\left\{\begin{array}{l}{x+1≠0}\\{(x-2)(x+1)≤0}\end{array}\right.$,
求得-1<x≤2,可得不等式的解集为(-1,2],
故选:A.
点评 本题主要考查分式不等式的解法,体现了等价转化的数学思想,属于基础题.

练习册系列答案
相关题目
1.甲、乙两个粮库要项A,B量诊运送大米,已知甲库将调出100吨大米,乙库将调出80吨大米,A镇至少需要60吨大米,B镇至少需要100吨大米,且甲往B镇运送大米的吨数不少于乙往A镇运送大米的吨数的2倍,两库到两镇运费如表(其中a为常数,$\frac{1}{2}$<a<2).
为了满足上述要求,同时使总运费最省,试问甲、乙粮库应运往A镇各多少吨大米?
| 运费(元/吨) | ||
| 甲库 | 乙库 | |
| A镇 | 240+10a | 180 |
| B镇 | 260 | 210 |
19.在一定的储存温度范围内,某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系y=ekx+b(e=2.71828…为自然对数的底数,k、b为常数).若该食品在0℃的保鲜时间为200小时,在30℃的保鲜时间是25小时,则该食品在20℃的保鲜时间是( )
| A. | 40小时 | B. | 50小时 | C. | 60小时 | D. | 80小时 |
20.直线2(m+1)x+(m-3)y-5m-1=0与圆(x-1)2+y2=3的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 无法判断 |
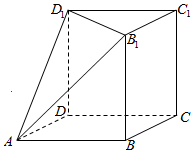 如图所示的几何体是由棱长为2cm的正方体ABCD一A1B1C1D1被平面AB1D1所截得的较大部分
如图所示的几何体是由棱长为2cm的正方体ABCD一A1B1C1D1被平面AB1D1所截得的较大部分