题目内容
12.已知f(x)是定义在R上的函数,且满足①f(4)=0;②曲线y=f(x+1)关于点(-1,0)对称;③x∈(-4,0)时,f(x)=log2($\frac{x}{{e}^{|x|}}$+ex-m).若y=f(x)在x∈[-4,4]上恰有7个零点,则实数m的取值范围为( )| A. | (-∞,-e-2) | B. | (-1-e-2,-e-2) | C. | (-1-e-2,0) | D. | (-1-e-2,-1-3e-4) |
分析 可判断f(x)在R上是奇函数,从而可化为当x∈(-4,0)时,f(x)=log2($\frac{x}{{e}^{|x|}}$+ex-m)有两个零点,从而转化为xex+ex-m=1在(-4,0)上有两个不同的解,再令g(x)=xex+ex-m-1,从而求导确定函数的单调性及取值范围,从而解得.
解答 解:∵曲线y=f(x+1)关于点(-1,0)对称;
∴曲线y=f(x)关于点(0,0)对称;
∴f(x)在R上是奇函数,
∴f(0)=0,
又∵f(4)=0,
∴f(-4)=0,
而y=f(x)在x∈[-4,4]上恰有7个零点,
故x∈(-4,0)时,f(x)=log2($\frac{x}{{e}^{|x|}}$+ex-m)有两个零点,
而f(x)=log2($\frac{x}{{e}^{|x|}}$+ex-m)
=log2($\frac{x}{{e}^{|x|}}$+ex-m)
=log2(xex+ex-m),
故xex+ex-m=1在(-4,0)上有两个不同的解,
令g(x)=xex+ex-m-1,
g′(x)=ex+xex+ex=ex(x+2),
故g(x)在(-4,-2)上是减函数,在(-2,0)上是增函数;
而g(-4)=-4e-4+e-4-m-1,g(0)=1-m-1=-m,g(-2)=-2e-2+e-2-m-1,
而g(-4)<g(0),
故-2e-2+e-2-m-1<0<-4e-4+e-4-m-1,
故-1-e-2<m<-1-3e-4,
故选:D.
点评 本题考查了导数的综合应用及函数的性质的判断与应用,同时考查了方程的根与函数的零点的关系应用.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
2.已知二项式(3-x)n(n∈N*)展开式中所有项的系数之和为a,所有项的系数的绝对值之和为b,则$\frac{b}{a}$+$\frac{a}{b}$的最小值为( )
| A. | $\frac{9}{2}$ | B. | 2 | C. | $\frac{13}{6}$ | D. | $\frac{5}{2}$ |
4.函数y=$\sqrt{lo{g}_{2}(2x-1)}$的定义域是( )
| A. | ($\frac{1}{2}$,1) | B. | ($\frac{1}{2}$,1] | C. | ($\frac{1}{2}$,+∞) | D. | [1,+∞) |
1.甲、乙两个粮库要项A,B量诊运送大米,已知甲库将调出100吨大米,乙库将调出80吨大米,A镇至少需要60吨大米,B镇至少需要100吨大米,且甲往B镇运送大米的吨数不少于乙往A镇运送大米的吨数的2倍,两库到两镇运费如表(其中a为常数,$\frac{1}{2}$<a<2).
为了满足上述要求,同时使总运费最省,试问甲、乙粮库应运往A镇各多少吨大米?
| 运费(元/吨) | ||
| 甲库 | 乙库 | |
| A镇 | 240+10a | 180 |
| B镇 | 260 | 210 |
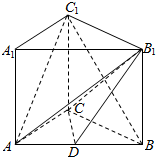 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=4,BC=3,AB=5,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=4,BC=3,AB=5,AA1=4,点D是AB的中点.