题目内容
已知关于x的方程|x2-4x+b|=c（b，c＞0）恰有三个不同实根x1，x2，x3，且x1+x2+x3=6，则b+c= ．
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：问题转化为y=|x2-4x+b|与y=c有三个不同交点，由二次函数的性质作出图象可得．
解答：
解：由二次函数的知识可知函数y=|x2-4x+b|的对称轴为x=2，（如图）
当且仅当-（22-4×2+b）=c即b+c=4时，y=|x2-4x+b|与y=c有三个不同交点，
∴关于x的方程|x2-4x+b|=c（b，c＞0）恰有三个不同实根时，b+c=4
故答案为：4．
解：由二次函数的知识可知函数y=|x2-4x+b|的对称轴为x=2，（如图）当且仅当-（22-4×2+b）=c即b+c=4时，y=|x2-4x+b|与y=c有三个不同交点，
∴关于x的方程|x2-4x+b|=c（b，c＞0）恰有三个不同实根时，b+c=4
故答案为：4．
点评：本题考查根的存在性及个数的判断，数形结合是解决问题的关键，属中档题．
练习册系列答案
相关题目
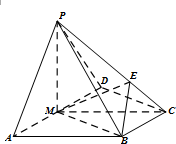如图，在四棱锥P-ABCD中，侧面PAD是正三角形，底面ABCD是直角梯形，AD∥BC，∠ADC=90°，AD=2BC=2，CD=
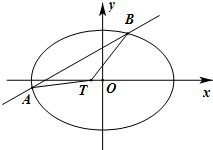如图，椭圆C：