题目内容
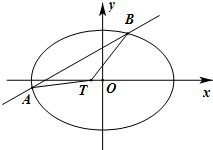 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知A,B为椭圆上两点,直线AB与坐标轴不垂直.设T(x0,0),若|AT|=|BT|,且|AB|=2,求x0的取值范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件得
+
=1,a2=2b2,由此能求出椭圆C的方程.
(Ⅱ)设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+m.把直线AB方程代入
+y2=1,得(2k2+1)x2+4kmx+2m2-2=0,由此利用韦达定理结合已知条件能求出x0的取值范围.
| 1 |
| a2 |
| 1 |
| 2b2 |
(Ⅱ)设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+m.把直线AB方程代入
| x2 |
| 2 |
解答:
解:(Ⅰ)∵椭圆C:
+
=1,(a>b>0)经过点(1,
),
∴
+
=1,…(2分)
又由t=
,得a2=2b2,…(4分)
代入上式得a=
,b=1,
故椭圆C的方程为
+y2=1.…(5分)
(Ⅱ)设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+m.
把直线AB方程代入
+y2=1,得(2k2+1)x2+4kmx+2m2-2=0,
∴由韦达定理得x1+x2=
,x1x2=
,
其中△=8(2k2+1-m2)>0,(7分)
∵|AB|=2,∴|AB|=
|x1-x2|=
=2,
化简得m2=
.…(*)…(9分)
设AB中点为G(xG,yG),故xG=
=
,yG=
,
∵|AT|=|BT|,∴点T在线段AB的中垂线上,
故直线GT的方程为y-
=-
(x+
),
令y=0得x0=
,即x02=
,(11分)
把(*)代入得x02=
=
.…(13分)
又△=8(2k2+1-m2)=
>0恒成立,
即k∈R.
故x02≤
,即x0∈[-
,
].
∴x0的取值范围为[-
,
].…(15分)
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴
| 1 |
| a2 |
| 1 |
| 2b2 |
又由t=
| ||
| 2 |
代入上式得a=
| 2 |
故椭圆C的方程为
| x2 |
| 2 |
(Ⅱ)设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+m.
把直线AB方程代入
| x2 |
| 2 |
∴由韦达定理得x1+x2=
| -4km |
| 2k2+1 |
| 2m2-2 |
| 2k2+1 |
其中△=8(2k2+1-m2)>0,(7分)
∵|AB|=2,∴|AB|=
| k2+1 |
2
| ||||||
| 2k2+1 |
化简得m2=
| 2k2+1 |
| 2(k2+1) |
设AB中点为G(xG,yG),故xG=
| x1+x2 |
| 2 |
| -2km |
| 2k2+1 |
| m |
| 2k2+1 |
∵|AT|=|BT|,∴点T在线段AB的中垂线上,
故直线GT的方程为y-
| m |
| 2k2+1 |
| 1 |
| k |
| 2km |
| 2k2+1 |
令y=0得x0=
| -km |
| 2k2+1 |
| k2m2 |
| (2k2+1)2 |
把(*)代入得x02=
| k2 |
| 2(2k2+1)(k2+1) |
| 1 | ||
2(2k2+
|
又△=8(2k2+1-m2)=
| 4(2k2+1)2 |
| k2+1 |
即k∈R.
故x02≤
3-2
| ||
| 2 |
2-
| ||
| 2 |
2-
| ||
| 2 |
∴x0的取值范围为[-
2-
| ||
| 2 |
2-
| ||
| 2 |
点评:本题考查椭圆方程的求法,考查点的横坐标的取值范围的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目