题目内容
已知直线l过点P(2,3),根据下列条件分别求出直线l的方程:
(1)l在x轴、y轴上的截距之和等于0;
(2)l与两条坐标轴在第一象限所围城的三角形面积为16.
(1)l在x轴、y轴上的截距之和等于0;
(2)l与两条坐标轴在第一象限所围城的三角形面积为16.
考点:直线的一般式方程
专题:直线与圆
分析:本题(1)分类写出直线的方程,根据要求条件参数的值;(2)写出直线的截距式方程,根据要求条件参数的值,得到本题结论.
解答:
解:(1)①当直线l经过原点时在x轴、y轴上的截距之和等于0,
此时直线l的方程为y=
x,
②当直线l经不过原点时,设直线l的方程为
+
=1(a≠0)
∵P(2,3)在直线l上,
∴
+
=1,
a=-1,即x-y+1=0.
综上所述直线l的方程为3x-2y=0或x-y+1=0.
(2)设l在x轴、y轴上的截距分别为a,b(a>0,b>0),
则直线l的方程为
+
=1
∵P(2,3)在直线l上,
∴
+
=1.
又由l与两条坐标轴在第一象限所围成的三角形面积为16,
可得ab=32,
∴a=8,b=4或a=
,b=12.
∴直线l的方程为
+
=1或
+
=1.
综上所述直线l的方程为x+2y-8=0或9x+2y-24=0.
此时直线l的方程为y=
| 3 |
| 2 |
②当直线l经不过原点时,设直线l的方程为
| x |
| a |
| y |
| -a |
∵P(2,3)在直线l上,
∴
| 2 |
| a |
| 3 |
| -a |
a=-1,即x-y+1=0.
综上所述直线l的方程为3x-2y=0或x-y+1=0.
(2)设l在x轴、y轴上的截距分别为a,b(a>0,b>0),
则直线l的方程为
| x |
| a |
| y |
| b |
∵P(2,3)在直线l上,
∴
| 2 |
| a |
| 3 |
| b |
又由l与两条坐标轴在第一象限所围成的三角形面积为16,
可得ab=32,
∴a=8,b=4或a=
| 8 |
| 3 |
∴直线l的方程为
| x |
| 8 |
| y |
| 4 |
| 3x |
| 8 |
| y |
| 12 |
综上所述直线l的方程为x+2y-8=0或9x+2y-24=0.
点评:本题考查了几种形式的直线方程,本题难度不大,属于基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
已知实数a,b,c满足a+b+c=1,a2+b2+c2=1,则a+b的取值范围是( )
| A、[-1,1] | ||
B、[-
| ||
C、[0,
| ||
| D、[0,2] |

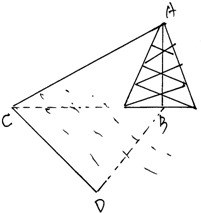 如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,则塔高AB=
如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,则塔高AB=