题目内容
已知数列{an}的各项均为正数,数列{bn},{cn}满足bn=
,cn=anan+12.
(1)若数列{an}为等比数列,求证:数列{cn}为等比数列;
(2)若数列{cn}为等比数列,且bn+1≥bn,求证:数列{an}为等比数列.
| an+2 |
| an |
(1)若数列{an}为等比数列,求证:数列{cn}为等比数列;
(2)若数列{cn}为等比数列,且bn+1≥bn,求证:数列{an}为等比数列.
考点:等比关系的确定,等差关系的确定
专题:等差数列与等比数列
分析:(1)由数列{an}为等比数列可得
=q,结合cn=anan+12可得:
=
=q3为常数,即数列{cn}为等比数列;
(2)由数列{cn}是等比数列可得
=q,即
=
=
=q,结合bn=
可得bn+22=bn+1•bn由bn+1≥bn,可得:bn+2=bn+1=bn,即
=
,即an+3=an+1•
,进而an+12=an•an+2,即数列{an}为等比数列.
| an+1 |
| an |
| cn+1 |
| cn |
an+1•
| ||
an
|
(2)由数列{cn}是等比数列可得
| cn+1 |
| cn |
| cn+1 |
| cn |
an+1•
| ||
an
|
| ||
an
|
| an+2 |
| an |
| an+3 |
| an+1 |
| an+2 |
| an |
| an+2 |
| an |
解答:
证明:(1)因为数列{an}为等比数列,所以
=q(q为常数),
又因为cn=anan+12.
所以
=
=q3为常数,所以数列{cn}为等比数列;
(2)因为数列{cn}是等比数列,所以
=q(q为常数),
所以
=
=
=q(q为常数),
则
=
,
所以
=
,
∵bn=
,
故bn+22=bn+1•bn.
因为bn+1≥bn,所以bn+2≥bn+1,则bn+22≥bn+12≥bn+1•bn.
所以bn+2=bn+1=bn.
∴
=
,即an+3=an+1•
.
因为数列{cn}是等比数列,所以
=
,即
=
,
把an+3=an+1•
代入化简得an+12=an•an+2,
所以数列{an}为等比数列.
| an+1 |
| an |
又因为cn=anan+12.
所以
| cn+1 |
| cn |
an+1•
| ||
an
|
(2)因为数列{cn}是等比数列,所以
| cn+1 |
| cn |
所以
| cn+1 |
| cn |
an+1•
| ||
an
|
| ||
an
|
则
| ||
an
|
| ||
an+2
|
所以
| ||
|
| an+2•an+3 | ||
an
|
∵bn=
| an+2 |
| an |
故bn+22=bn+1•bn.
因为bn+1≥bn,所以bn+2≥bn+1,则bn+22≥bn+12≥bn+1•bn.
所以bn+2=bn+1=bn.
∴
| an+3 |
| an+1 |
| an+2 |
| an |
| an+2 |
| an |
因为数列{cn}是等比数列,所以
| cn+1 |
| cn |
| cn+2 |
| cn+1 |
| ||
an
|
| ||
an+1
|
把an+3=an+1•
| an+2 |
| an |
所以数列{an}为等比数列.
点评:本题考查的知识点是等比数列关系的确定,转化比较困难,运算量比较大,属于中档题.

练习册系列答案
相关题目
已知实数a,b,c满足a+b+c=1,a2+b2+c2=1,则a+b的取值范围是( )
| A、[-1,1] | ||
B、[-
| ||
C、[0,
| ||
| D、[0,2] |
一组数据中每个数据都减去50构成一组新数据,则这组新数据的平均数是1.2,方差是4.4,则原来一组数的方差为( )
| A、3.2 | B、4.4 |
| C、4.8 | D、5.6 |
已知函数y=Asin(ωx+φ的图象如图所示,则该函数的解析式可能是( )
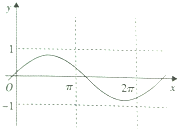

A、y=
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=
|
 如图所示,已知A1B1C1-ABC是三棱柱,E、E1分别是AC、A1C1的中点.求证:平面AB1E1∥平面BEC1.
如图所示,已知A1B1C1-ABC是三棱柱,E、E1分别是AC、A1C1的中点.求证:平面AB1E1∥平面BEC1.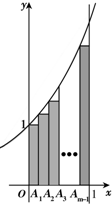 如图,A1,A2,…,Am-1(m≥2)为区间[0,1]上的m等分点,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1,图中m个矩形构成的阴影区域为Ω2,在Ω1中任取一点,则该点取自Ω2的概率等于
如图,A1,A2,…,Am-1(m≥2)为区间[0,1]上的m等分点,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1,图中m个矩形构成的阴影区域为Ω2,在Ω1中任取一点,则该点取自Ω2的概率等于