题目内容

（1）化简(a
2
3
b
1
2
)(-3a
1
2
b
1
3
)÷(
1
3
a
1
6
b
5
6
)
（2）计算 log225•log34•log59．
考点：对数的运算性质
专题：函数的性质及应用
分析：（1）利用指数的运算法则即可得出．
（2）利用对数的运算法则即可得出．
解答： 解：（1）原式=
-3
1
3
a
2
3
+
1
2
-
1
6
b
1
2
+
1
3
-
5
6
=-9a．
（2）原式=
2lg5
lg2
•
2lg2
lg3
•
2lg3
lg5
=8．
点评：本题考查了指数与对数的运算法则，属于基础题．
练习册系列答案
相关题目
已知偶函数f（x）满足f（x+2）=f（x），当x∈（O，1）时，f（x）=2x，则f（log
1
2
5）=
 
．
点（2，1）到直线3x+4y+5=0的距离是（　　）
A、3
B、
5
7
C、
7
25
D、
25
7
已知
a
与
b
不共线，向量
a
+
b
与2
a
-
b
垂直，
a
-2
b
与2
a
+
b
也垂直，求
a
与
b
的夹角的余弦值．
在△ABC中，BC边的中点M（-
5
2
，
1
2
），直线AC的方程为x+1=0，直线AB的方程为x+y-1=0，求直线BC的直线方程．
设点A（-2，3），B（2，4），直线l过点P（-1，1），且与线段AB相交，求直线l的斜率的取值范围．
已知集合A={x||x-1|＞2}，B={y|y=x+
1
x
，x∈R且x≠0}，则（∁RB）∩A=（　　）
A、（-2，3]
B、[-2，3]
C、（-2，-1）
D、[-2，-1）
设集合A={x||x-a|≤2}，B={x||x-1|≥3}，若A∩B=∅，那么a的取值范围是（　　）
A、a≥2或a≤0
B、0≤a≤2
C、0≤a≤1
D、0＜a＜2
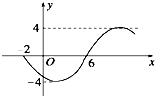函数f（x）=Asin（ωx+φ），（A＞0，ω＞0，x∈R）的部分图象如右图所示，则函数的表达式为（　　）
A、f（x）=4sin（
π
4
x+
3π
8
）
B、f（x）=4sin（
π
4
x-
3π
8
）
C、f（x）=4sin（
π
8
x-
3π
4
）
D、f（x）=4sin（
π
8
x+
π
8
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网