Question

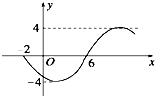函数f（x）=Asin（ωx+φ），（A＞0，ω＞0，x∈R）的部分图象如右图所示，则函数的表达式为（　　）

• A、f（x）=4sin（

  π

  4

  x+

  3π

  8

  ）
• B、f（x）=4sin（

  π

  4

  x-

  3π

  8

  ）
• C、f（x）=4sin（

  π

  8

  x-

  3π

  4

  ）
• D、f（x）=4sin（

  π

  8

  x+

  π

  8

  ）

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：根据函数的图象确定A，ω 和φ的值即可求该函数的解析式．

解答： 解：由图象知A=4，函数的周期T=2×[6-（-2）]=16．
即

2π

ω

=16，则ω=

π

8

，
即f（x）=4sin（

π

8

x+φ），
由图象知f（2）=-4，
即4sin（

π

8

×2+φ）=-4，
则sin（

π

4

+φ）=-1，
即

π

4

+φ=-

π

2

+2kπ，
则φ=-

3π

4

+2kπ，
则f（x）=4sin（

π

8

x-

3π

4

+2kπ）=4sin（

π

8

x-

3π

4

），
故选：C

点评：本题主要考查三角函数解析式的求解，利用条件确定A，ω 和φ的值是解决本题的关键．