题目内容
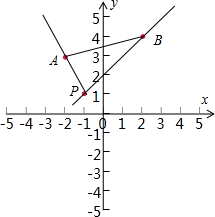
设点A(-2,3),B(2,4),直线l过点P(-1,1),且与线段AB相交,求直线l的斜率的取值范围.
考点:斜率的计算公式
专题:直线与圆
分析:先根据A,B,P的坐标分别求得直线AP和BP的斜率,设L与线段AB交于M点,M由A出发向B移动,斜率越来越大,期间会出现AM平行y轴,此时无斜率.求得k的一个范围,过了这点M,斜率由-∞增大到直线BP的斜率K.求得k的另一个范围,最后综合可得答案.
解答:
 解:直线AP的斜率k=
解:直线AP的斜率k=
=-2,直线BP的斜率k=
=1.
设L与线段AB交于M点,M由B出发向A移动,斜率越来越大,
在某点处会AM平行y轴,此时无斜率.即k≥1,
过了这点,斜率由-∞增大到直线BP的斜率-2.即k≤-2,
直线l斜率取值范围为(-∞,-2]∪[1,+∞).
 解:直线AP的斜率k=
解:直线AP的斜率k=| 3-1 |
| -2+1 |
| 4-1 |
| 2+1 |
设L与线段AB交于M点,M由B出发向A移动,斜率越来越大,
在某点处会AM平行y轴,此时无斜率.即k≥1,
过了这点,斜率由-∞增大到直线BP的斜率-2.即k≤-2,
直线l斜率取值范围为(-∞,-2]∪[1,+∞).
点评:本题主要考查了直线的斜率,解题的关键是利用了数形结合、转化思想,解题过程较为直观.

练习册系列答案
相关题目
下列给出的对象中,能组成集合的是( )
| A、一切很大的数 |
| B、无限接近于0的数 |
| C、美丽的小女孩 |
| D、方程x2-1=0的实数根 |
已知集合M={y|y=x2+2x-3,x∈R},集合N={x|-5≤x≤2},则M∩(∁RN)等于( )
| A、[-4,+∞) |
| B、(-∞,-5)∪(2,+∞) |
| C、(2,+∞) |
| D、∅ |
已知实数a,b,c,d满足
=
=1,则(a-c)2+(b-d)2的最小值为( )
| lna |
| b |
| d2-2d |
| -c2 |
A、
| ||||
B、2-
| ||||
C、3-2
| ||||
D、1-
|
