题目内容
已知椭圆C:
+
=1(a>b>0)的右顶点A,上顶点为B,F1为左焦点,M为椭圆上一点,MF1垂直于x轴,O为坐标原点且
与
共线,又直线l:(k+2)x-2ky+4k+8=0(k∈R),过定点P,且P恰在椭圆的左准线上.
(1)求定点P的坐标;
(2)求椭圆C的方程;
(3)设直线l与直线MF1的交点为Q,当k为何值时以PQ为直径的圆过点B?
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| OM |
(1)求定点P的坐标;
(2)求椭圆C的方程;
(3)设直线l与直线MF1的交点为Q,当k为何值时以PQ为直径的圆过点B?
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:探究型,圆锥曲线的定义、性质与方程
分析:对第(1)问,将直线l的方程中的k分离出来,根据定点不随k的改变而改变,即可获得定点.
对第(2)问,由P点在椭圆的左准线上,得a与c的等量关系;由MF1垂直于x轴,可设M(-c,y0),利用
与
共线的充要条件,得y0的表达式,再将点M的坐标代入椭圆方程中,得a,c的另一个关系,联立关于a,c的两个方程,可得a,c的值,从而得b2,即得椭圆的标准方程.
对第(3)问,设Q点的坐标为(-2,y1),可用y1表示
的坐标,而
的坐标可求,由
⊥
,得关于y1的方程,可得y1的值,由两点的斜率公式,得直线PQ的斜率,即为直线l的斜率,由l的方程得关于k的方程,即可得k的值.
对第(2)问,由P点在椭圆的左准线上,得a与c的等量关系;由MF1垂直于x轴,可设M(-c,y0),利用
| AB |
| OM |
对第(3)问,设Q点的坐标为(-2,y1),可用y1表示
| BQ |
| BP |
| BP |
| BQ |
解答:
解:(1)直线l的方程变形为k(x-2y+4)+2x+8=0,
由于l过定点P,则当k变化时,上式恒成立,所以
,
得
,即定点P的坐标为(-4,0).
(2)由点P(-4,0)在椭圆的左准线x=-
上知,-
=-4,得a2=4c.…①
由MF1垂直于x轴,可设M(-c,y0),则
=(-c,y0),
易知,
=(-a,b),由
与
共线,得-bc=-ay0,即y0=
,从而M(-c,
),
又M在椭圆上,将M的坐标代入椭圆方程中,得
+
=1,化简得a2=2c2.…②
由①、②,得c=2,a2=8,从而b2=a2-c2=4.
故椭圆C的方程为
+
=1.
(3)由(2)知,直线MF1的方程为x=-2,
由于Q点在直线MF1上,可设Q点的坐标为(-2,y1),则
=(-2,y1-2),
易知,
=(-4,-2),当
⊥
时,以PQ为直径的圆过点B,
此时,
•
=0,得(-4,-2)•(-2,y1-2)=0,解得y1=6,即Q(-2,6).
由两点的斜率公式,得直线PQ的斜率=
=3,
又由l的方程知,l的斜率=
,
所以
=3,解得k=
,
即当k为
时,以PQ为直径的圆过点B.

由于l过定点P,则当k变化时,上式恒成立,所以
|
得
|
(2)由点P(-4,0)在椭圆的左准线x=-
| a2 |
| x |
| a2 |
| c |
由MF1垂直于x轴,可设M(-c,y0),则
| OM |
易知,
| AB |
| AB |
| OM |
| bc |
| a |
| bc |
| a |
又M在椭圆上,将M的坐标代入椭圆方程中,得
| (-c)2 |
| a2 |
(
| ||
| b2 |
由①、②,得c=2,a2=8,从而b2=a2-c2=4.
故椭圆C的方程为
| x2 |
| 8 |
| y2 |
| 4 |
(3)由(2)知,直线MF1的方程为x=-2,
由于Q点在直线MF1上,可设Q点的坐标为(-2,y1),则
| BQ |
易知,
| BP |
| BP |
| BQ |
此时,
| BP |
| BQ |
由两点的斜率公式,得直线PQ的斜率=
| 6-0 |
| -2-(-4) |
又由l的方程知,l的斜率=
| k+2 |
| 2k |
所以
| k+2 |
| 2k |
| 2 |
| 5 |
即当k为
| 2 |
| 5 |
点评:本题考查了直线的方程,椭圆的方程,圆的性质等,关键是将“以PQ为直径的圆过点B”转化为两直线的垂直问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合M={x|x-2<0},N={x|x<a},若M⊆N,则实数a的取值范围是( )
| A、[2,+∞) |
| B、(2,+∞) |
| C、(-∞,0) |
| D、(-∞,0] |
已知命题:p:在△ABC中,sinA>sinB的充分不必要条件是A>B;q:?x∈R,x2+2x+2≤0.则下列命题为真命题的是( )
| A、p∧q | B、¬p∧q |
| C、¬p∨q | D、p∨q |
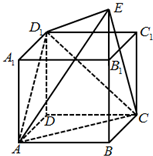 如图长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,|BB1|=a,E为BB1延长线上的一点且满足|BB1|•|B1E|=1.
如图长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,|BB1|=a,E为BB1延长线上的一点且满足|BB1|•|B1E|=1.